Dấu hiệu chia hết cho 8 rất đơn giản: một số chia hết cho 8 khi ba chữ số cuối của số đó chia hết cho 8.
Nội dung dưới đây tổng hợp lý thuyết ngắn gọn, bài tập có lời giải chi tiết và mẹo ghi nhớ nhanh, giúp học sinh nắm chắc kiến thức và áp dụng chính xác trong mọi dạng bài.
.png)
Video bài giảng
Các dấu hiệu chia hết cho 8 cần nhớ
Có 4 cách để nhận biết một số tự nhiên có chia hết cho 8 hay không, bao gồm:
|
Các dấu hiệu |
Ví dụ |
|
1. a. Nếu chữ số hàng trăm là chẵn, thì số tạo thành bởi hai chữ số sau cùng phải chia hết cho 8. b. Nếu chữ số hàng trăm là lẻ, thì số tạo thành bởi hai chữ số sau cùng cộng thêm 4 phải được số chia hết cho 8. |
a. Số 624 có chữ số hàng trăm là 6 và là số chẵn 2 chữ số sau cùng là 24 chia hết cho 8 => 624 chia hết cho 8 b. Số 352 có chữ số hàng trăm là 3 và là số lẻ 2 chữ số sau cùng là 52, cộng 4 là 56 - là số chia hết 8 => Số 352 chia hết cho 8. |
|
2. Cộng chữ số sau cùng vào hai lần phần còn lại. Giá trị thu được phải là bội của 8. |
Số 56 có chữ số sau cùng là 6. Phần còn là 5 Ta có: 6 + 5 x 2 = 16 là bội của 8 => 56 chia hết cho 8 |
|
3. Ba chữ số sau cùng tạo thành số chia hết cho 8 |
1624. Ba chữ số cuối là 624. Ta có: 624 : 8 = 78 không dư => 1624 chia hết cho 8 |
|
4. Cộng 4 lần chữ số hàng trăm vào 2 lần chữ số hàng chục và 1 lần chữ số hàng đơn vị được kết quả phải là bội của 8. |
Số 34152 Chữ số hàng trăm là 1 Chữ số hàng chục là 5 Chữ số hàng đơn vị là 2 Ta có: 4 x 1 + 2 x 5 + 1 x 2 = 16 là bội của 8 => 34152 chia hết cho 8. |
Các số chia hết cho 8 thường gặp trong đề thi
1. Các số tròn trăm, tròn nghìn: 1000, 2000, 4000, 8000… (vì 000 luôn chia hết cho 8).
2. Các số tròn chục đặc biệt: 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96.
3. Các số có ba chữ số cuối quen thuộc: 112, 120, 136, 144, 152, 168, 176, 184, 192.
4. Các số lớn xuất hiện trong bài toán thực tế: 240, 320, 400, 480, 560, 640, 720, 800, 880, 960.
5. Các số “bẫy” thường gặp: 008, 016, 072, 104, 208, 312, 416, 512, 616, 712, 816, 912.
Các dạng bài tập dấu hiệu hết cho 8
Có x dạng bài về dấu hiệu chia hết cho 8. Dưới đây là mô tả và hướng dẫn phương pháp giải cho mỗi dạng bài. Bé hãy đọc kỹ phần kiến thức và ví dụ mẫu để nắm được cách làm đúng.
Dạng 1: Kiểm tra 1 số có chia hết cho 8 không

Đề bài: Kiểm tra trong 1 dãy số cho trước những số nào chia hết cho 8, những số nào không chia hết cho 8.
a. Số nào chia hết cho 8
b. Số nào không chia hết cho 8
Phương pháp giải:
| Căn cứ vào 1 trong 4 dấu hiệu kể trên, thực hiện phép tính để xác định số đó có chia hết cho 8 hay không. Lưu ý: Dấu hiệu 1, 3 và 4 chỉ áp dụng cho số có 3 chữ số trở lên. |
Ví dụ: Cho dãy số 42, 48, 156; 336, 457 hãy xác định:
a. Số nào chia hết cho 8
b. Số nào không chia hết cho 8
Lời giải:
a. Áp dụng dấu hiệu chia hết cho 8 số 2: Cộng chữ số sau cùng vào hai lần phần còn lại. Giá trị thu được phải là bội của 8 (do 2 số đầu không có chữ số hàng trăm), ta có:
|
42 |
2 + 2 x 4 = 10 không là bội của 8 |
|
48 |
8 + 2 x 4 = 16 là bội của 8 |
|
156 |
6 + 15 x 2 =36 không là bội của 8 |
|
336 |
6 + 33 x 2 = 72 là bội của 8 |
|
457 |
7 + 45 x 2 = 97 không là bội của 8 |
Vậy các số chia hết cho 8 là: 48 & 336
b. Dựa vào kết quả câu a, các số không chia hết cho 8 là 42; 156; 457
Dạng 2: Từ các số cho trước thành lập số chia hết cho 8

Đề bài: Cho các số: 1, 2,3.... Hãy viết các số có (x) chữ số chia hết cho 8
Phương pháp giải:
|
Các bước giải:
Bước 1: Gọi số cần lập là ab, abc,... tùy theo yêu cầu số chữ số trong đề bài.
Bước 2: Áp dụng các dấu hiệu chia hết cho 8 để lập số.
TH1: Nếu đề bài yêu cầu lập số có 2 chữ số, bé áp dụng dấu hiệu 2
Giả sử số có 2 chữ số là ab.
Áp dụng dấu hiệu 2, ta có:
ab chia hết cho 8 => (b + 2a) chia hết cho 8 (cũng tức là bội của 8)
Nếu a = …. => b = …. sao cho thỏa mãn điều kiện (b + 2a) chia hết cho 8 => ab = … là số chia hết cho 8.
TH2: Nếu đề bài yêu cầu lập số có 3 chữ số, bé áp dụng dấu hiệu 1 hoặc 2
Giả sử số có 3 chữ số là abc.
|
Các dấu hiệu |
Cách áp dụng |
|
Dấu hiệu 1 |
Nếu a chẵn thì (bc) phải chia hết cho 8 Nếu a lẻ thì (bc + 4) phải chia hết cho 8 |
|
Dấu hiệu 2 |
abc chia hết cho 8 khi (c + 2 x ab) chia hết cho 8 |
TH3: Nếu đề bài yêu cầu lập số có từ 4 chữ số trở lên, áp dụng 1 trong 4 dấu hiệu
Giả sử đề bài yêu cầu lập số có 4 chữ số thì số đó có dạng: abcd.
|
Các dấu hiệu |
Cách áp dụng |
|
Dấu hiệu 1 |
Nếu b chẵn thì (cd) phải chia hết cho 8 Nếu b lẻ thì (cd + 4) phải chia hết cho 8 |
|
Dấu hiệu 2 |
abc chia hết cho 8 khi (d + 2 x abc) chia hết cho 8 |
|
Dấu hiệu 3 |
Thực hiện phép tính (bcd) chia cho 8, nếu không dư thì abcd chia hết cho 8. |
|
Dấu hiệu 4 |
Thực hiện phép tính: (4 x b + 2 x c + d) chia hết cho 8 |
Ví dụ: Cho các số 2, 4, 6, 9. Hãy lập các số có 3 chữ số chia hết cho 8
Lời giải:
Giả sử số có 3 chữ số là abc.
TH1: Áp dụng dấu hiệu 1, ta có:
Nếu a = 2 là số chẵn => abc chia hết cho 8 khi (bc) chia hết cho 8.
Lần lượt thay b bằng các số đã cho, ta có:
b = 2 thì c = 4 => bc = 24 chia hết cho 8 => abc = 224
b = 4 thì c không có giá trị thỏa mãn
b = 6 thì c = 4 => bc = 64 chia hết cho 8 => abc = 264
b = 9 thì c = 6 => bc = 96 chia hết cho 8 => abc = 296
Ta có các số thỏa mãn là: 224; 264; 296.
Nếu a = 4 là số chẵn, lần lượt thay b bằng các số đã cho ta có các số thỏa mãn: 424; 464; 496
Nếu a = 6 là số chẵn, lần lượt thay b bằng các số đã cho ta có các số thỏa mãn: 624; 664; 696
Nếu a = 9 là số lẻ => abc chia hết cho 8 khi (bc + 4) chia hết cho 8.
Lần lượt thay b bằng các số đã cho, ta có:
b = 2 => (2c + 4) chia hết cho 8 => c không có giá trị nào thỏa mãn
b = 4 => (4c + 4) chia hết cho 8 => c = 4 => abc = 944
b = 6 => (6c + 4) chia hết cho 8 => c = 9 => abc = 969
b = 9 => (9c + 4) chia hết cho 8 => c = 2 => abc = 992
Ta có các số thỏa mãn là: 944; 969; 992.
Vậy các số có 3 chữ số chia hết cho 8 gồm: 224; 264; 296; 424; 464; 496; 624; 664; 696; 944; 969; 992.
TH2: Áp dụng dấu hiệu 2
abc chia hết cho 8 khi: (c + 2 x ab) chia hết cho 8. Lần lượt thay a, b, c bằng các số đã cho, ta có bảng sau:
|
Giá trị của c |
Giá trị của b |
Giá trị của a |
Phép tính |
Chia hết cho 8 |
|
2 |
2 |
2 |
2 + 2 x 22 = 46 |
không |
|
2 |
2 |
4 |
2 + 2 x 24 = 50 |
không |
|
2 |
2 |
6 |
2 + 2 x 26 = 54 |
không |
|
2 |
2 |
9 |
2 + 2 x 92 = 186 |
không |
|
2 |
4 |
2 |
2 + 2 x 24 = 50 |
không |
|
2 |
4 |
4 |
2 + 2 x 44 = 90 |
không |
|
2 |
4 |
6 |
2 + 2 x 64 = 130 |
không |
|
2 |
4 |
9 |
2 + 2 x 94 = 190 |
không |
|
2 |
6 |
2 |
2 + 2 x 26 = 54 |
không |
|
2 |
6 |
4 |
2 + 2 x 46 = 94 |
không |
|
2 |
6 |
6 |
2 + 2 x 66 = 134 |
không |
|
2 |
6 |
9 |
2 + 2 x 96 = 194 |
không |
|
2 |
9 |
2 |
2 + 2 x 29 = 60 |
không |
|
2 |
9 |
4 |
2 + 2 x 49 = 100 |
không |
|
2 |
9 |
6 |
2 + 2 x 69 = 140 |
không |
|
2 |
9 |
9 |
2 + 2 x 99 = 200 |
Không |
Áp dụng tương tự với các giá trị c = 4, c = 6 và c = 9, ta có kết quả như áp dụng dấu hiệu 1.
Dạng 3: Điền số thích hợp để tạo thành số chia hết cho 8

Đề bài: Cho 1 số tự nhiên gồm 2 phần: 1 phần các chữ số đã biết và 1 phần chưa biết.
Phương pháp giải:
| Áp dụng 1 trong 4 dấu hiệu chia hết cho 8 để tìm được giá trị thỏa mãn. Các số có thể điền trong phạm vi từ 0 - 9 hoặc có giới hạn tùy đề bài. |
Ví dụ: Cho số 35ab. Hãy điền 2 chữ số thay thế a và b để tạo thành số chia hết cho 8.
Áp dụng dấu hiệu 1:
35ab có chữ số hàng trăm là 5 và là số lẻ
=> 35ab chia hết cho 8 khi (ab + 4) chia hết cho 8
Nếu a = 1 => (1b + 4) chia hết cho 8 => b = 2 => ab = 12 => 35ab = 3512
Nếu a = 2 => (2b + 4) chia hết cho 8 => b = 0; 8 => ab = 20; 28 => 35ab = 3520; 3528
Nếu a = 3 => (3b + 4) chia hết cho 8 => b = 6 => ab = 36 => 35ab = 3536
Nếu a = 4 => (4b + 4) chia hết cho 8 => b = 4 => ab = 44 => 35ab = 3544
Nếu a = 5 => (5b + 4) chia hết cho 8 => b = 2 => ab = 52 => 35ab = 3552
Nếu a = 6 => (6b + 4) chia hết cho 8 => b = 0 => ab = 60 => 35ab = 3560
Nếu a = 7 => (7b + 4) chia hết cho 8 => b = 6 => ab = 76 => 35ab = 3576
Nếu a = 8 => (8b + 4) chia hết cho 8 => b = 4 => ab = 84 => 35ab = 3584
Nếu a = 9 => (9b + 4) chia hết cho 8 => b = 2 => ab = 92 => 35ab = 3592
Áp dụng dấu hiệu 2:
35ab chia hết cho 8 khi: (b + 2 x 35a) chia hết cho 8
Nếu a = 1 => (b + 2 x 351) = (b + 702) chia hết cho 8 => b = 2
Nếu a = 2 => (b + 2 x 352) = (b + 704) chia hết cho 8 => b = 0; 8
Thực hiện tương tự ta tìm được các số như áp dụng dấu hiệu 1.
Áp dụng dấu hiệu 3:
35ab chia hết cho 8 khi: 5ab chia hết cho 8
Nếu a = 1 => 51b chia hết cho 8 khi b = 2 => 51b = 512 => 35ab = 3512
Thực hiện tương tự ta tìm được các số như áp dụng dấu hiệu 1.
Áp dụng dấu hiệu 4:
35ab chia hết cho 8 khi: (4 x 5 + 2 x a + b) chia hết cho 8
Nếu a = 1 => (4 x 5 + 2 x a + b) = (4 x 5 + 2 x 1 + b) = (22 + b) chia hết cho 8 khi b = 2
=> ab = 12 => 35ab = 3512.
Thực hiện tương tự ta tìm được các số như áp dụng dấu hiệu 1.
Bài tập dấu hiệu chia hết cho 8 CÓ LỜI GIẢI
Sau khi nắm được các kiến thức cơ bản, ba mẹ hãy cùng bé làm bài tập dưới đây nhé!
Bài tập dấu hiệu chia hết cho 8 theo dạng
Bài 1: Số nào chia hết cho 8?

Bài 2: Cho dãy các số 38562; 71096; 9384; 2541; 6473; 5981, hãy xác định:
a. Số nào chia hết cho 8?
b. Số nào không chia hết cho 8?
Bài 3: Chọn 1 số thích hợp điền vào chỗ trống để tạo thành số chia hết cho 8:
a. 856__
b. 582__8
c. 43__56
d. 94__2
Bài 4: Một nhà máy sản xuất kẹo có 26.936 viên kẹo cần xuất xưởng 8 gói. Liệu sau khi quá trình đóng gói hoàn thành thì nhà máy còn kẹo không?
Bài 5: Nếu Maria đóng gói 8 quả táo trong một túi, liệu cô ấy có thể đóng gói 1.848 quả táo trong những túi như vậy mà không để sót quả táo nào không?
Lời giải & Đáp án bài tập dấu hiệu chia hết cho 8
Bài 1:
|
STT |
Số |
Số chia hết cho 8 không |
STT |
Số |
Số chia hết cho 8 không |
|
1 |
40019 |
không |
2 |
145729 |
không |
|
3 |
80128 |
có |
4 |
42104 |
có |
|
5 |
24790 |
không |
6 |
9985 |
không |
|
7 |
308448 |
có |
8 |
6032 |
có |
|
9 |
531 |
không |
10 |
72995 |
không |
|
11 |
987936 |
có |
12 |
624 |
có |
|
13 |
11378 |
không |
14 |
308725 |
không |
|
15 |
734200 |
có |
16 |
256 |
có |
|
17 |
61473 |
không |
18 |
8144 |
có |
Bài 2:
a. Áp dụng dấu hiệu 1, ta có:
38562: Số hàng trăm lẻ, 62 + 4 = 66 không chia hết cho 8 => 38562 không chia hết cho 8
71096: Số hàng trăm chẵn, 96 chia hết cho 8 => 71096 chia hết cho 8
9384: Số hàng trăm lẻ, 84 + 4 = 88 chia hết cho 8 => 9384 chia hết cho 8
2541: Số hàng trăm lẻ, 41 + 4 = 45 không chia hết cho 8 => 2541 không chia hết cho 8
6473: Số hàng trăm chẵn, 73 không chia hết cho 8 => 6473 không chia hết cho 8
5981: Số hàng trăm lẻ, 81 + 4 = 85 không chia hết cho 8 => 5981 không chia hết cho 8
=> Các số chia hết cho 8 là: 71096 & 9384
b. Từ kết quả câu a, các số không chia hết cho 8 là: 38562; 2541; 6473; 5981
Bài 3:
a. 856__
Áp dụng dấu hiệu 1, số hàng trăm là 5 và là số lẻ
=> 856__ chia hết cho 8 khi (6__ + 4) chia hết cho 8
=> Số cần điền là: 0; 8
=> Số chia hết cho 8 là 8560 & 8568
b. 582__8
Áp dụng dấu hiệu 1, số hàng trăm chẵn => __8 chia hết cho 8
=> Số cần điền là 4; 8
=> Số chia hết cho 8 là 58248 & 58288
c. 43__56
Áp dụng dấu hiệu 4, ta có:
(4 x __ + 2 x 5 + 6) chia hết cho 8 => (4 x __ + 16) chia hết cho 8
Nếu __ = 1 => (4 x __ + 16) = (4 x 1 + 16) = 20 không chia hết cho 8
Nếu __ = 2 => (4 x __ + 16) = (4 x 2 + 16) = 24 chia hết cho 8
Nếu __ = 3 => (4 x __ + 16) = (4 x 3 + 16) = 28 không chia hết cho 8
Nếu __ = 4 => (4 x __ + 16) = (4 x 4 + 16) = 32 chia hết cho 8
Nếu __ = 5 => (4 x __ + 16) = (4 x 5 + 16) = 36 không chia hết cho 8
Nếu __ = 6 => (4 x __ + 16) = (4 x 6 + 16) = 40 chia hết cho 8
Nếu __ = 7 => (4 x __ + 16) = (4 x 7 + 16) = 44 không chia hết cho 8
Nếu __ = 8 => (4 x __ + 16) = (4 x 8 + 16) = 48 chia hết cho 8
Nếu __ = 9 => (4 x __ + 16) = (4 x 9 + 16) = 52 không chia hết cho 8
=> Số cần điền là: 2; 4; 6; 8
=> Số chia hết cho 8 là: 43256; 43456; 43656; 43956.
d. 94__2
Áp dụng dấu hiệu 1, số hàng trăm chẵn => __2 chia hết cho 8
=> Số cần điền là: 3; 7
=> Số chia hết cho 8 là: 9432 & 9472
Bài 4:
Để sau khi quá trình đóng gói hoàn thành không còn kẹo thì tổng số kẹo phải chia hết cho 8, tức là 26936 phải chia hết cho 8.
Xét số 26936 có số hàng trăm là lẻ, 36 + 4 = 40 chia hết cho 8 => 26936 chia hết cho 8.
Vậy không còn kẹo sau khi đóng gói.
Bài 5:
Maria có thể đóng được số táo trên mà không sót quả nào nếu tổng số táo chia hết cho 8.
Áp dụng dấu hiệu 1, số 1848 có số hàng trăm là chẵn, 48 chia hết cho 8
=> 1848 chia hết cho 8
=> Maria có thể sắp xếp 8 quả táo vào mỗi túi mà không sót quả nào.


Dạy bé học toán lớp 4 tại nhà, bố mẹ đã biết cách giúp bé học vui học tốt?

Phép chia là gì? Tổng hợp kiến thức cơ bản nhất trong phép chia
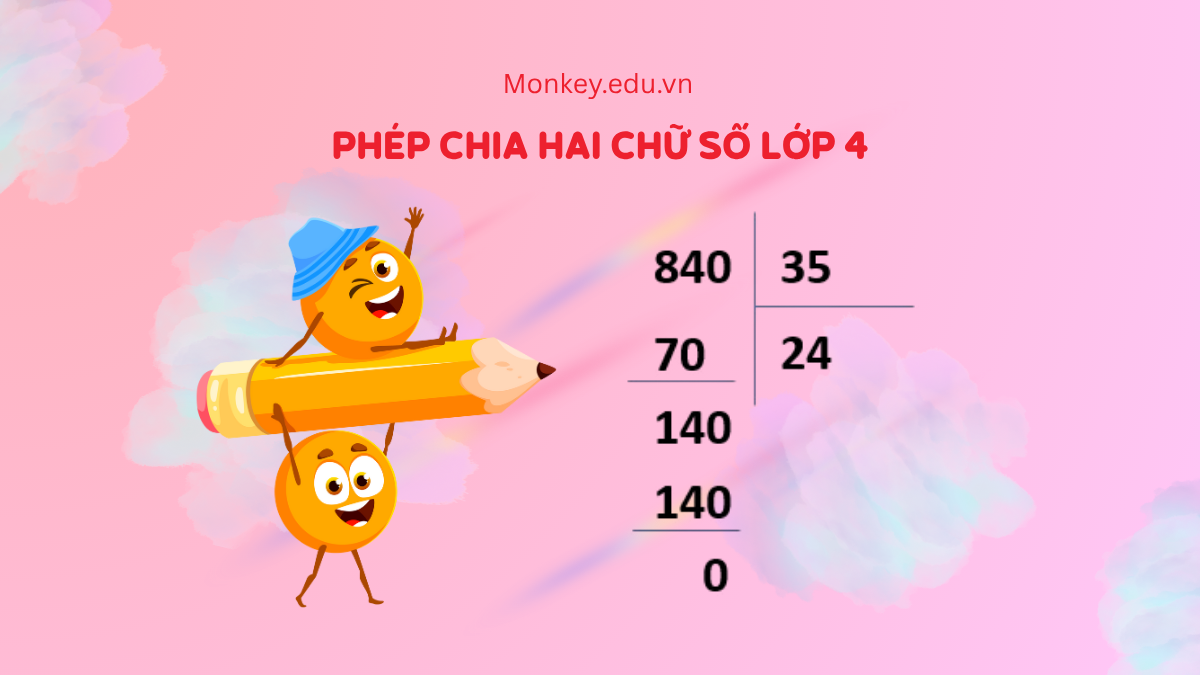
Phép chia hai chữ số lớp 4: Cách tính & Bài tập (có đáp án)
Dấu hiệu chia hết cho các số tự nhiên khác
| Số | Dấu hiệu chia hết |
| Dấu hiệu chia hết cho 4 | 2 chữ số cuối của số đó chia hết cho 4. |
| Dấu hiệu chia hết cho 5 | Chữ số tận cùng là 0 hoặc 5. |
| Dấu hiệu chia hết cho 6 | Số đó chia hết cho 2 và chia hết cho 3. |
| Dấu hiệu chia hết cho 7 | Lấy chữ số cuối × 2, rồi lấy phần còn lại trừ kết quả; nếu được số chia hết cho 7 thì số ban đầu chia hết cho 7. |
| Dấu hiệu chia hết cho 10 | Chữ số tận cùng là 0. |
| Dấu hiệu chia hết cho 11 | Tổng các chữ số ở vị trí chẵn – tổng các chữ số ở vị trí lẻ, nếu kết quả chia hết cho 11 → số chia hết cho 11. |
| Dấu hiệu chia hết cho 12 | Số đó chia hết cho 3 và chia hết cho 4. |
| Dấu hiệu chia hết cho 13 | Lấy chữ số cuối × 4, cộng vào phần còn lại; nếu được số chia hết cho 13 thì số ban đầu chia hết cho 13. |
| Dấu hiệu chia hết cho 15 | Số đó chia hết cho 3 và chia hết cho 5. |
| Dấu hiệu chia hết cho 18 | Số đó chia hết cho 2 và chia hết cho 9. |
| Dấu hiệu chia hết cho 24 | Số đó chia hết cho 3 và chia hết cho 8. |
| Dấu hiệu chia hết cho 25 | 2 chữ số cuối là 00, 25, 50 hoặc 75. |
Cách ghi nhớ dấu hiệu chia hết trong Toán học
Dấu hiệu chia hết cho 8, cho 2,... là phần kiến thức cơ bản quan trọng giúp các con thực hiện phép nhân, phép chia nhanh & chính xác. Đây cũng là nền tảng để các con học tốt phần Phân số ở chương sau.
Để ghi nhớ các dấu hiệu này, ba mẹ cần ôn tập cùng bé với những bí quyết dưới đây:
1. Đọc kĩ kiến thức & tự đặt ví dụ
Trước khi làm các bài tập Luyện tập hay vở bài tập, các con cần đọc lại bài giảng trong Sách giáo khoa 1 - 2 lần để nhớ lại bài học trên lớp. Tiếp đến, với mỗi phần kiến thức nhỏ, con hãy tự đặt ví dụ và giải thích. Phần này bé cần ba mẹ đồng hành để kiểm tra độ chính xác.
2. Tự thực hiện bài tập một mình
Sau khi đã nắm vững các dấu hiệu chia hết, con hãy tự hoàn thành bài tập mà không có sự hướng dẫn của cha mẹ. Qua phần tự thực hành, phụ huynh có thể đánh giá được mức độ hiểu bài của con.
3. Kiểm tra đúng sai và giải thích chi tiết
Sau khi con hoàn thành bài tập, ba mẹ hãy cùng con kiểm tra đúng sai. Đối với những câu đúng, ba mẹ có thể chọn 1 số câu bất kỳ để hỏi con cách giải.
Ví dụ: Với bài tập điền số chia hết cho 8, hãy hỏi vì sao con điền số X (số bé đã điền)?
Đối với các câu sai, hãy yêu cầu con nghĩ thêm và viết lại đáp án. Nếu con chưa làm đúng, hãy giải thích kỹ và hướng dẫn con giải với nhịp điệu chậm để con dễ tiếp thu.
4. Kết hợp các phương pháp học toán khác
Ngoài học qua sách vở, phụ huynh nên cho con thử phương pháp học toán mới qua chương trình học Toán điện tử. Một trong số các chương trình học Toán chuẩn theo chương trình của Bộ Giáo dục qua ứng dụng trên điện thoại phổ biến hiện nay là Monkey Math.
Các bài học trên Monkey được tổng hợp theo các chủ đề: Phép cộng, phép trừ, đếm số từ 1 - 10, từ 10 - 100, 100 - 1000; phép nhân chia; hình học; đo lường, thời gian, phép tính hệ thập phân, v.v…. Mỗi bài gồm phần lý thuyết kèm ví dụ minh họa, sau đó là chuỗi bài tập dạng hoạt động tương tác giúp con ghi nhớ bài hiệu quả. Chương trình có đầy đủ 60+ chủ đề toán học xuyên suốt chương trình Tiểu học hỗ trợ con đạt điểm tốt hơn trên lớp.
Tính đến nay, con số phụ huynh học sinh trong cộng đồng Monkey đã lên tới hàng triệu. Đây là nơi ba mẹ được học hỏi và chia sẻ phương pháp dạy con cho 3 môn chính là Toán, Văn, Anh. Vì vậy, tham gia cộng đồng, ba mẹ có thể sẵn sàng trở thành giáo viên tại nhà của con bất cứ lúc nào.
5. Sử dụng sách bổ trợ toán học
Bên cạnh học lý thuyết và luyện bài tập trên SGK, VBT, ba mẹ có thể sưu tầm thêm 1 số sách bài tập mở rộng, bài tập nâng cao tùy theo trình độ của con để học thêm. Cùng với đó, nếu ba mẹ đăng ký học Toán với Monkey Math cũng sẽ được nhận bộ 3 sách bài tập bổ trợ kèm theo để bé nâng cao kiến thức của mình.
FAQ - Những thắc mắc khác về dấu hiệu chia hết cho 8
1. Vì sao phải xét 3 chữ số cuối mà không phải toàn bộ số?
Vì 1000 chia hết cho 8, nên chỉ cần kiểm tra phần dư là ba chữ số cuối.
2. Số có ít hơn 3 chữ số thì áp dụng thế nào?
Chỉ cần lấy chính số đó đem chia cho 8, không cần tách.
3. Nếu ba chữ số cuối có số 0 thì có ảnh hưởng không?
Không ảnh hưởng, chỉ cần lấy đúng ba chữ số cuối rồi kiểm tra phép chia.
4. Có cần làm phép chia dài để kiểm tra không?
Không. Chỉ cần xem ba chữ số cuối có thuộc bảng số chia hết cho 8 (như 008, 016, 024, 032...) hoặc tính nhẩm nhanh.
5. Số âm có áp dụng dấu hiệu chia hết cho 8 không?
Có. Chỉ xét ba chữ số cuối của phần giá trị tuyệt đối rồi xác định kết quả.
Qua bài học này, bé đã nắm được kiến thức về dấu hiệu chia hết cho 8 và ứng dụng tốt trong các bài tập. Hãy kết hợp việc học qua sách giáo khoa và sách điện tử trên điện thoại Monkey Math để con tự nâng cao kiến thức và đạt điểm tốt trên lớp nhé!
1. Divisibility Rule for 8 Worksheets - Ngày truy cập: 9/12/25
https://www.tutoringhour.com/worksheets/divisibility-rules/for-8/
2. Divisibility 8 - Ngày truy cập: 9/12/25
https://www.liveworksheets.com/worksheet/en/math/1745306







.png)
.png)







.png)