Chuyên đề số phức ôn thi THPT Quốc Gia môn Toán: Lý thuyết & Bài tập

Chuyên đề số phức trong cấu trúc đề thi Toán THPT Quốc Gia 2024

Dựa trên đề thi tham khảo môn Toán do Bộ GD&ĐT công bố, trong cấu trúc đề thi Toán THPT Quốc Gia 2024 thì chuyên đề số phức chiếm khoảng 6 câu hỏi, trong đó có 4 câu thuộc mức độ nhận biết và thông hiểu, 2 câu thuộc mức độ vận dụng và vận dụng cao. Chính vì vậy, việc ôn tập kỹ lưỡng các kiến thức về số phức là vô cùng quan trọng đối với các thi sinh tham gia kỳ thi THPT Quốc Gia 2024.

Kiến thức tổng quát về chuyên đề số phức ôn thi THPT Quốc Gia

Dưới đây là tất cả các kiến thức về chuyên đề số phức trong đề thi THPT Quốc Gia đã được Monkey tóm gọn, giúp cho các thí sinh dễ dàng ôn tập hơn.

Khái niệm số phức

Số phức là một biểu thức có dạng a + bi, trong đó a, b là các số thực và số i thỏa mãn i2 = -1. 

Ký hiệu số phức là z, viết là z = a + bi.

Trong đó:

• i được gọi là đơn vị ảo

• a được gọi là phần thực, ký hiệu Re(z) = a

• b được gọi là phần ảo của số phức z = a + bi, ký hiệu Im(z) = b

• Tập hợp các số phức ký hiệu là C.

Lưu ý: 

• Mỗi số thực a dương đều được xem là số phức với phần ảo b = 0, z = a.

• Số phức z = a + bi có a = 0 được gọi là số thuần ảo hay là số ảo.

• Số 0 vừa là số thực vừa là số ảo.

Hai số phức bằng nhau

Cho z = a + bi và z’ = a’ + b’i.

Biểu diễn hình học của số phức

Mỗi số phức được biểu diễn bởi một điểm M(a;b) trên mặt phẳng toạ độ Oxy.

Ngược lại, mỗi điểm M(a;b) biểu diễn một số phức là z = a + bi .

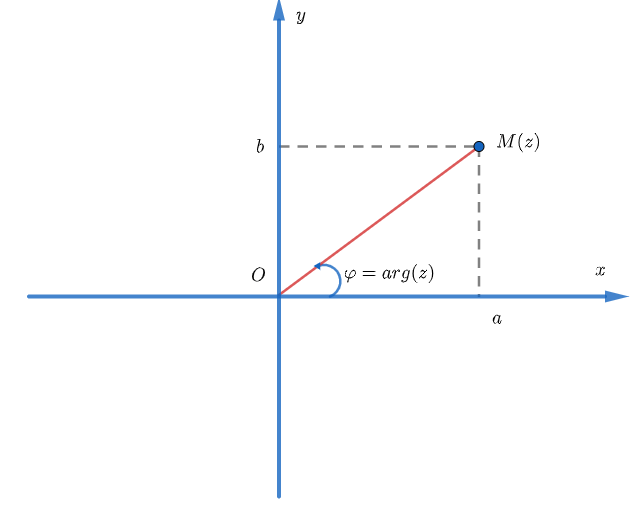
Phép cộng và phép trừ các số phức

Cho hai số phức z = a + bi và z’ = a’ + b’i. 

Nghĩa là:

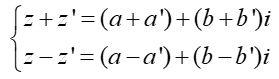
Phép nhân số phức

Cho hai số phức z = a + bi và z’ = a’ + b’i. 

Nghĩa là:

zz’ = aa’ - bb’ + (ab’ - a’b)i

Số phức liên hợp

Số phức liên hợp là một nội dung quan trọng thuộc chuyên đề về số phức mà các thí sinh cần lưu ý.

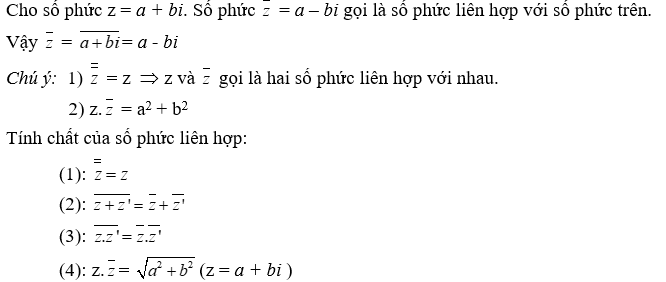
Môđun của số phức

Phép chia số phức khác 0

Cho số phức z = a + bi  ≠ 0 (tức là a2 + b2 > 0 )

Ta định nghĩa số nghịch đảo z-1 của số phức z ≠ 0, là số:

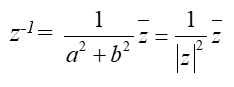
Thương z’/z của phép chia số phức z’ cho số phức z ≠ 0 được xác định như sau:

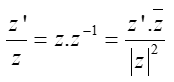
Các phép tính cộng, trừ, nhân chia số phức nói trên nó cũng có đầy đủ tính chất giao hoán, phân phối, kết hợp như các phép cộng, trừ, nhân, chia số thực thông thường.

Phương trình bậc hai với hệ số thực

Một số kết quả nhanh về số phức cần nhớ 

Dưới đây là phần tổng hợp số phức trong đề thi Đại Học với một số kết quả nhanh cần ghi nhớ, giúp các thí sinh có thể giải các câu hỏi một cách nhanh chóng và dễ dàng hơn.

1. i0 = 1 => i4n = 1

2. i1 = i => i4n+1 = i

3. i2 = -1 => i4n+2 = -1

4. i3 = - i => i4n+3 = -i

5. (1 - i)2 = -2i

6. (1 + i)2 = 2i

Hướng dẫn cách giải các dạng bài tập số phức thi THPT Quốc Gia

Monkey cung cấp cho thí sinh hướng dẫn cách giải các dạng bài tập về chuyên đề số phức ôn thi THPT Quốc Gia một cách chi tiết và nhanh chóng nhất.

Dạng 1: Tính toán các yếu tố của số phức

Tính toán các yếu tố của số phức là dạng bài tập số phức ôn thi THPT Quốc Gia đơn giản và dễ lấy điểm nhất mà các thí sinh nên lưu tâm.

Hướng dẫn: Đối với bài tập chuyên đề số phức dạng này, thí sinh cần sử dụng định nghĩa, các phép toán để tính toán các yếu tố có liên quan để tính toán các yếu tố khác nhau của số phức.

Ví dụ: Cho hai số phức z1 = 5 - 7i và z2 = 2 + 3i. Tìm số phức z = z1 + z2.

Hướng dẫn giải: 

z = z1 + z2 = (5 - 7i) + (2 + 3i) = 7 - 4i

Dạng 2: Phương trình trên tập số phức

Hướng dẫn: Sử dụng các phương pháp giải phương trình mẫu mực như phương trình bậc nhất, phương trình bậc hai….với ẩn là số phức z.

Ví dụ: 

Các bài viết không thể bỏ lỡ

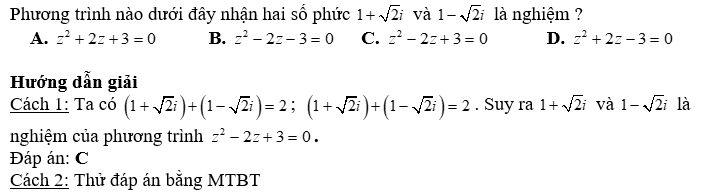
Cấu trúc đề thi Toán THPT Quốc Gia 2024 & Mẹo giải đề hiệu quả

Hướng dẫn cách tính giá trị biểu thức và bài tập vận dụng

Tổng hợp 10 kênh học toán lớp 5 miễn phí tốt nhất dành cho bé

Dạng 3: Tìm số phức thỏa mãn điều kiện

Hướng dẫn: Để giải bài toán tìm số phức thỏa mãn điều kiện cho trước, ta thực hiện theo các bước sau:

• Bước 1: Đặt z = a +bi (a,b thuộc R)
• Bước 2: Thay vào điều kiện để được hệ phương trình hai ẩn a,b.
• Bước 3: Giải tìm a,b.

Chú ý:

Ví dụ: 

Dạng 4: Biểu diễn hình học của số phức 

Hướng dẫn: Giả sử z = x + yi (x, y thuộc R). Khi đó số phức z biểu diễn trên mặt phẳng phức bởi điểm M(x;y). Các thí sinh có thể sử dụng dữ kiện của đề bài để tìm mối liên hệ giữa x và y từ đó suy ra tập hợp điểm M.

Một số quỹ tích thường gặp:

Với z = x + yi (x, y là các số thực) khi đó nếu:

x = a : Quỹ tích z là đường thẳng x = a (song song với Oy).

y = b: Quỹ tích z là đường thẳng y = b (song song với Ox).

(x - a)2 +( y - b)2 = R2 : Quỹ tích z là đường tròn tâm I(a.b) bán kính R.

(x - a)2 +( y - b)2 =< R2 : Quỹ tích z là hình tròn tâm I(a.b) bán kính R ( kể cả biên).

(x - a)2 +( y - b)2 >= R2 : Quỹ tích z là các điểm nằm ngoài đường tròn tâm I(a.b) bán kính R.

Ví dụ: Cho số phức z = 1 - 2i. Điểm nào dưới đây là điểm biểu diễn của số phức w = iz trên mặt phẳng tọa độ?

Hướng dẫn giải:

Ta có w = iz = i(1 - 2i) = 2 + i. Suy ra điểm biểu diễn của số phức w là N (2;1).

Đáp án: B

Dạng 5: Cực trị của số phức

Cực trị của số phức là một dạng bài toán thuộc chuyên đề số phức vận dụng cao mà các thí sinh cần đặc biệt quan tâm nếu như muốn đạt được số điểm từ 8 trở lên.

Hướng dẫn: Sử dụng các kiến thức cơ bản như: Bất đẳng thức liên hệ giữa trung bình cộng và trung bình nhân, bất đẳng thức Bunhia- Cốpxki, bất đẳng thức hình học và một số bài toán công cụ sau:

Bài toán công cụ 1:

Cho đường tròn (T) cố định có tâm I bán kính R và điểm A cố định. Điểm M di động trên đường tròn (T) . Hãy xác định vị trí điểm M sao cho AM lớn nhất, nhỏ nhất.

Hướng dẫn giải:

TH1: A thuộc đường tròn (T) 

Ta có: 

• AM đạt giá trị nhỏ nhất bằng 0 khi M trùng với A

• AM đạt giá trị lớn nhất bằng 2R khi M là điểm đối xứng với A qua I

TH2: A không thuộc đường tròn (T)

Gọi B, C là giao điểm của đường thẳng qua A,I và đường tròn (T); 

Giả sử AB < AC.

+ Nếu A nằm ngoài đường tròn (T) thì với điểm M bất kì trên (T), ta có:

AM >= AI - IM = AI - IB = AB, đẳng thức xảy ra khi M trùng B.

AM =< AI + IM = AI + IC = AC, đẳng thức xảy ra khi M trùng C.

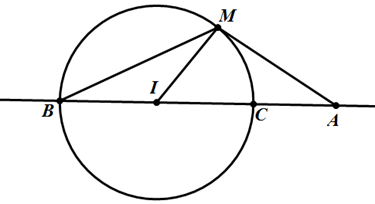
+ Nếu A nằm trong đường tròn (T) thì với điểm M bất kì trên (T), ta có:

AM >= IM - IA = IB - IA = AB, đẳng thức xảy ra khi M trùng B.

AM =< AI + IM = AI + IC = AC, đẳng thức xảy ra khi M trùng C.

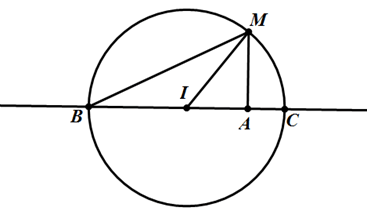
Vậy khi M trùng với B thì AM đạt giá trị nhỏ nhất, và khi M trùng với C thì AM đạt giá trị lớn nhất.

Xem thêm: Cấu trúc đề thi Toán THPT Quốc Gia 2024 & Mẹo giải đề hiệu quả

Bài toán công cụ 2:

Cho hai đường tròn (T1) có tâm I, bán kính R1; đường tròn (T2) có tâm J, bán kính R2. Tìm vị trí của điểm M trên (T1), điểm N trên (T2) sao cho MN đạt giá trị lớn nhất, nhỏ nhất.

Hướng dẫn giải:

Gọi d là đường thẳng đi qua I, J; d cắt đường tròn (T1) tại hai điểm phân biệt A, B (giả sử JA > JB) ; d cắt (T2) tại hai điểm phân biệt C, D (giả sử ID > IC).

Với điểm M bất kì trên (T1) và điểm N bất kì trên (T2).

Ta có: 

MN =< IM + IN =< IM + IJ + JN = R1 + R2 + IJ = AD, đẳng thức xảy ra khi M trùng với A và N trùng với D.

MN >= | IM - IN | >= |IJ - IM - JN| = |IJ - R1 + R2| = BC, đẳng thức xảy ra khi M trùng với B và N trùng với C.

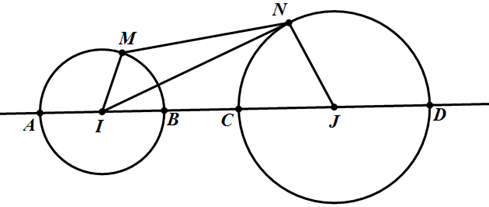
Vậy khi M trùng với A và N trùng với D thì MN đạt giá trị lớn nhất, và khi M trùng với B và N trùng với C thì MN đạt giá trị nhỏ nhất.

Bài toán công cụ 3: 

Cho hai đường tròn (T) có tâm I, bán kính R; đường thẳng [denta] không có điểm chung với (T). Tìm vị trí của điểm M trên (T), điểm N trên [denta] sao cho MN đạt giá trị nhỏ nhất.

Hướng dẫn giải:

Gọi H là hình chiếu vuông góc của I trên d.

Đoạn IH cắt đường tròn (T) tại J.

Với M thuộc đường thẳng [denta], N thuộc đường tròn (T), ta có: 

MN >= IN - IM >= IH - IJ = JH = const, đẳng thức xảy ra khi M trùng H và N trùng I.

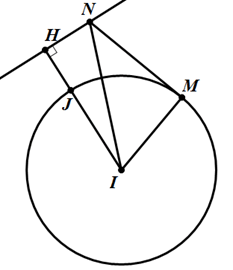
Vậy khi M trùng với H; N trùng với J thì MN đạt giá trị nhỏ nhất.

Với những kiến thức và kỹ năng về chuyên đề số phức được trang bị từ bài viết này của Monkey, bạn hoàn toàn có thể tự tin chinh phục điểm cao trong kỳ thi THPT Quốc Gia môn Toán. Hãy ôn tập thường xuyên, luyện tập giải đề liên tục và đừng quên tham khảo thêm các tài liệu ôn thi khác để củng cố kiến thức toàn diện. Chúc bạn học tập hiệu quả và đạt được kết quả tốt nhất trong kỳ thi!