Chuyên đề hàm số ôn thi THPT Quốc Gia môn Toán: Lý thuyết & Dạng bài tập!

Chuyên đề hàm số trong cấu trúc đề thi Toán THPT Quốc Gia 2024

Cấu trúc đề thi Toán THPT Quốc Gia 2024 bao gồm 50 câu hỏi trong đó 45 câu thuộc về kiến thức lớp 12 và 5 câu liên quan đến lớp 11. Đặc biệt, trong đề thi tham khảo THPT Quốc Gia 2024 môn Toán do Bộ GD&ĐT công bố, chuyên đề hàm số chiếm đến 10/50 số lượng câu hỏi. Điều này có nghĩa, chuyên đề hàm số lớp 12 chính là một nội dung vô cùng quan trọng mà các thí sinh cần phải ôn tập thật kỹ lưỡng.

Tính đơn điệu của hàm số

Tính đơn điệu của hàm số là một nội dung thuộc chuyên đề hàm số ôn thi THPT Quốc Gia cơ bản và dễ lấy điểm nhất.

Lý thuyết tính đơn điệu của hàm số

Dưới đây là chi tiết lý thuyết về tính đơn điệu của hàm số, gồm: Hàm số đơn điệu là gì? Điều kiện CẦN và ĐỦ để hàm số đơn điệu?

Dạng 1: Tính đơn điệu của hàm số có chứa tham số

Dạng 2: Tính đơn điệu của hàm phân thức

Đối với tính đơn điệu của hàm phân thức, chúng ta có thể chia nhỏ thành 3 dạng toán như sau:

Dạng 3: Tính đơn điệu của hàm số bậc ba

Để tính đơn điệu của hàm số bậc ba, chúng ta sẽ có những thông tin cơ bản sau:

Cho hàm số bậc ba: y = f(x) = ax3 + bx2 + cx + d (a ≠ 0)

• Tập xác định: D = R

• Đạo hàm: y’ = f(x)’ = 3ax2 + 2bx + c

Dạng 4: Tính đơn điệu của hàm tổng, hàm hợp, hàm liên kết

Xét tính đơn điệu của các hàm số tổng, hàm số hợp và hàm liên kết:

• Xét tính đơn điệu của hàm số: y = f(x) + g(x)

• Xét tính đơn điệu của hàm số: y = f(u(x)), với u là một hàm đối với biến x

Phương pháp giải:

• Bước 1: Tính đạo hàm y’ (nếu có)

• Bước 2: Giải các bất phương trình y’ > 0; y’ < 0 hoặc lập bảng xét dấu

• Bước 3: Đưa ra kết luận

Chú ý:

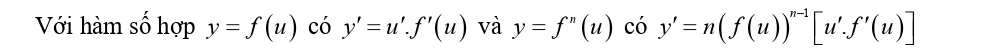
Dạng 5: Tính đơn điệu của hàm số chứa dấu giá trị tuyệt đối

Dạng toán tính đơn điệu của hàm số chứa dấu giá trị tuyệt đối được chia thành 2 trường hợp cụ thể như sau:

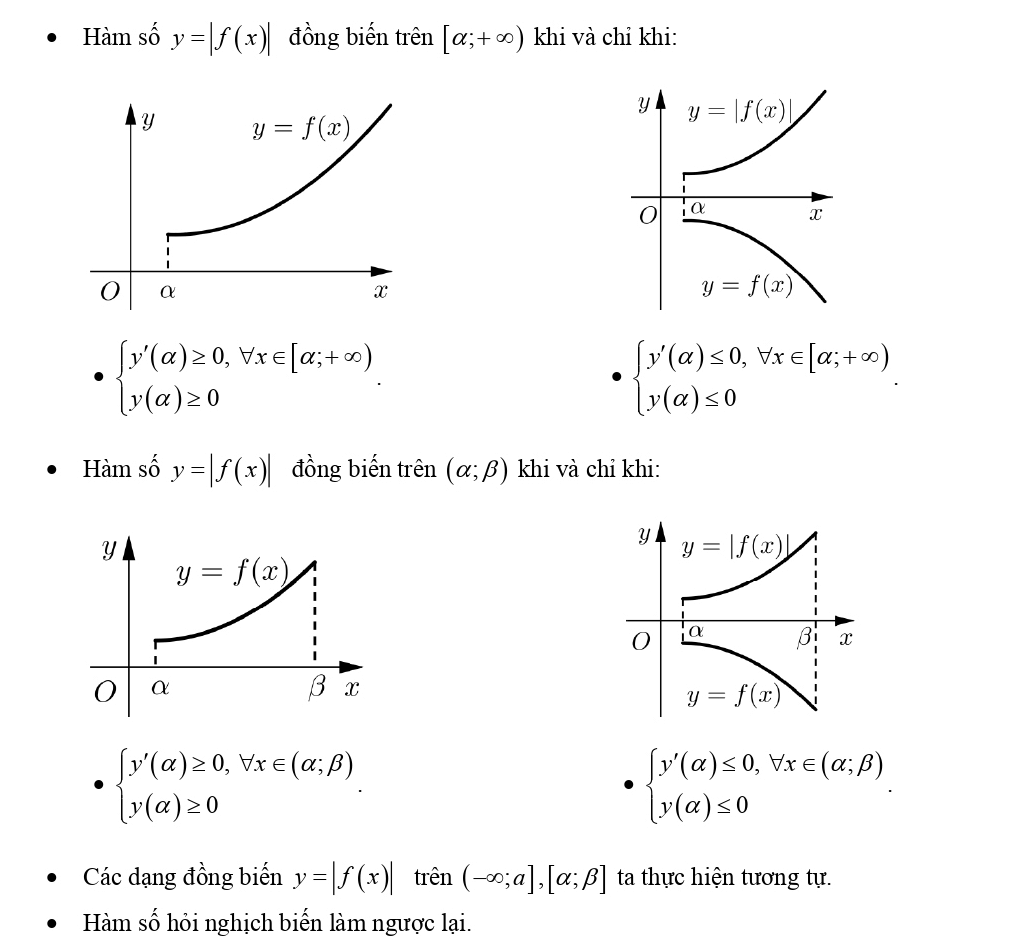
Cực trị của hàm số

Tiếp theo, các thí sinh cần nắm rõ cả lý thuyết và các dạng bài tập về chuyên đề cực trị của hàm số.

Lý thuyết cực trị của hàm số

Lý thuyết chuyên đề cực trị hàm số sẽ được Monkey trình bày lần lượt theo thứ tự từ định nghĩa đến quy tắc tìm cực trị như sau:

Từ định lí trên, ta có một quy tắc khác để tìm cực trị của hàm số, như sau:

Dạng 1: Cực trị hàm bậc ba

Bài toán tổng quát: Cho hàm số y = f(x) =  ax3 + bx2 + cx + d (a ≠ 0; a, b, c, d phụ thuộc vào tham số). Tìm giá trị của tham số để hàm số có cực đại, cực tiểu (cực trị) thỏa mãn điều kiện cho trước.

Phương pháp tổng quát:

Dạng 2: Cực trị hàm trùng phương

Bài toán tổng quát: Cho hàm số y = f(x) =  ax4 + bx2 + cx (a, b, c phụ thuộc vào tham số m. Tìm m để hàm số có 3 cực trị và thỏa mãn điều kiện cho trước.

Phương pháp tổng quát:

Dạng 3: Cực trị của hàm hợp

Kiến thức trọng tâm về cực trị của hàm hợp và phương pháp giải cụ thể như sau:

Đạo hàm của hàm hợp: [ f (u(x)) ]’ = u’(x).f’(u(x))

Tính chất đổi dấu của biểu thức: Gọi x = a là một nghiệm của phương trình f(x) = 0. Khi đó:

• Nếu x = a là nghiệm bội bậc chẵn {(x - a)2 ; (x - a)4 ;...} thì hàm số y = f(x) không đổi dấu khi đi qua a.

• Nếu x = a là nghiệm đơn hoặc nghiệm bội bậc lẻ {(x - a) ; (x - a)3 ;...} thì hàm số y = f(x) đổi dấu khi đi qua a.

Để tìm cực trị của hàm số y = [ f (u(x)) ] ta làm như sau:

• Bước 1: Tính đạo hàm y’ = [ f (u(x)) ]’

• Bước 2: Giải phương trình y’ = [ f (u(x)) ]’ = 0 dựa vào đồ thị hay bảng biến thiên của hàm số y = f(x).

• Bước 3: Lập bảng biến thiên của hàm số

• Bước 4: Kết luận về các điểm cực trị

Dạng 4: Cực trị hàm số chứa dấu giá trị tuyệt đối

Một số kiến thức về dạng toán cực trị hàm số chứa dấu giá trị tuyệt đối mà thí sinh cần nắm như sau:

Các bài viết không thể bỏ lỡ

Cấu trúc đề thi Toán THPT Quốc Gia 2024 & Mẹo giải đề hiệu quả

Chuyên đề số phức ôn thi THPT Quốc Gia môn Toán: Lý thuyết & Bài tập

Tổng hợp 7 website học toán online lớp 5 tốt nhất dành cho bé

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Trong chuyên đề hàm số ôn thi THPT Quốc Gia, giá trị lớn nhất và giá trị nhỏ nhất của hàm số được đánh giá là có khả năng xuất hiện trong đề thi cao hơn hẳn.

Dưới đây là phần tóm tắt lý thuyết giá trị lớn nhất và giá trị nhỏ nhất của hàm số:

Định nghĩa:

Các phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất:

1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bằng cách khảo sát trực tiếp

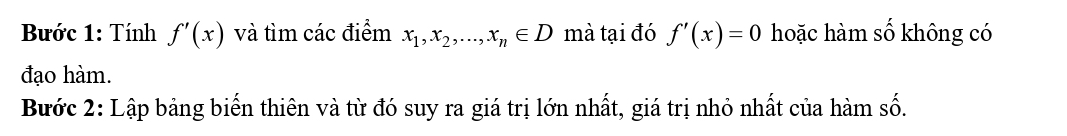
2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn

3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng

Bất đẳng thức trị tuyệt đối:

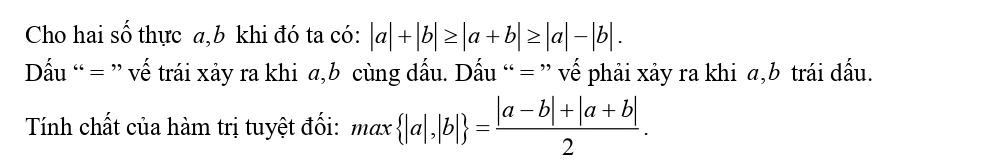
Phương pháp chung để giải các bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số chứa dấu giá trị tuyệt đối:

Tiệm cận của đồ thị hàm số

Tóm tắt lý thuyết tiệm cận của đồ thị hàm số:

1. Đường tiệm cận ngang

2. Đường tiệm cận đứng

3. Dấu hiệu nhận biết các đường tiệm cận của đồ thị hàm số

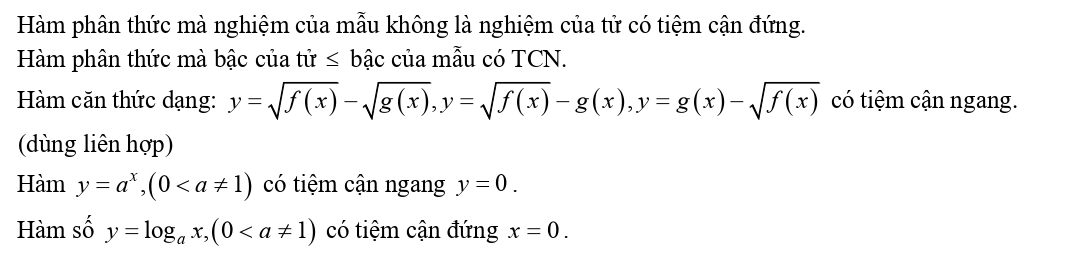
4. Cách tìm các đường tiệm cận của đồ thị hàm số

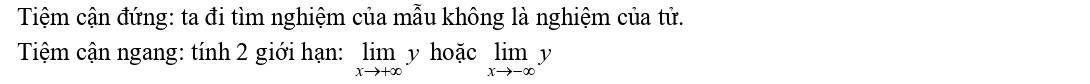
5. Một số chú ý trong quá trình tìm tiệm cận

Các dạng toán về đường tiệm cận của đồ thị hàm số có thể xuất hiện trong đề thi THPT Quốc Gia, bao gồm:

• Dạng 1: Đường tiệm cận của đồ thị hàm số bậc nhất trên bậc nhất

• Dạng 2: Đường tiệm cận của đồ thị hàm số phân thức hữu tỉ

• Dạng 3: Đường tiệm cận của đồ thị hàm số căn thức

• Dạng 4: Tìm đường tiệm cận của đồ thị hàm số dựa vào đồ thị, bảng biến thiên

Nhận diện hàm số và biến đổi đồ thị

Các dấu hiệu giúp bạn dễ dàng nhận diện hàm số và biến đổi đồ thị của một số hàm đa thức và phân thức:

1. Hàm số bậc ba y =  ax3 + bx2 + cx + d (a ≠ 0)

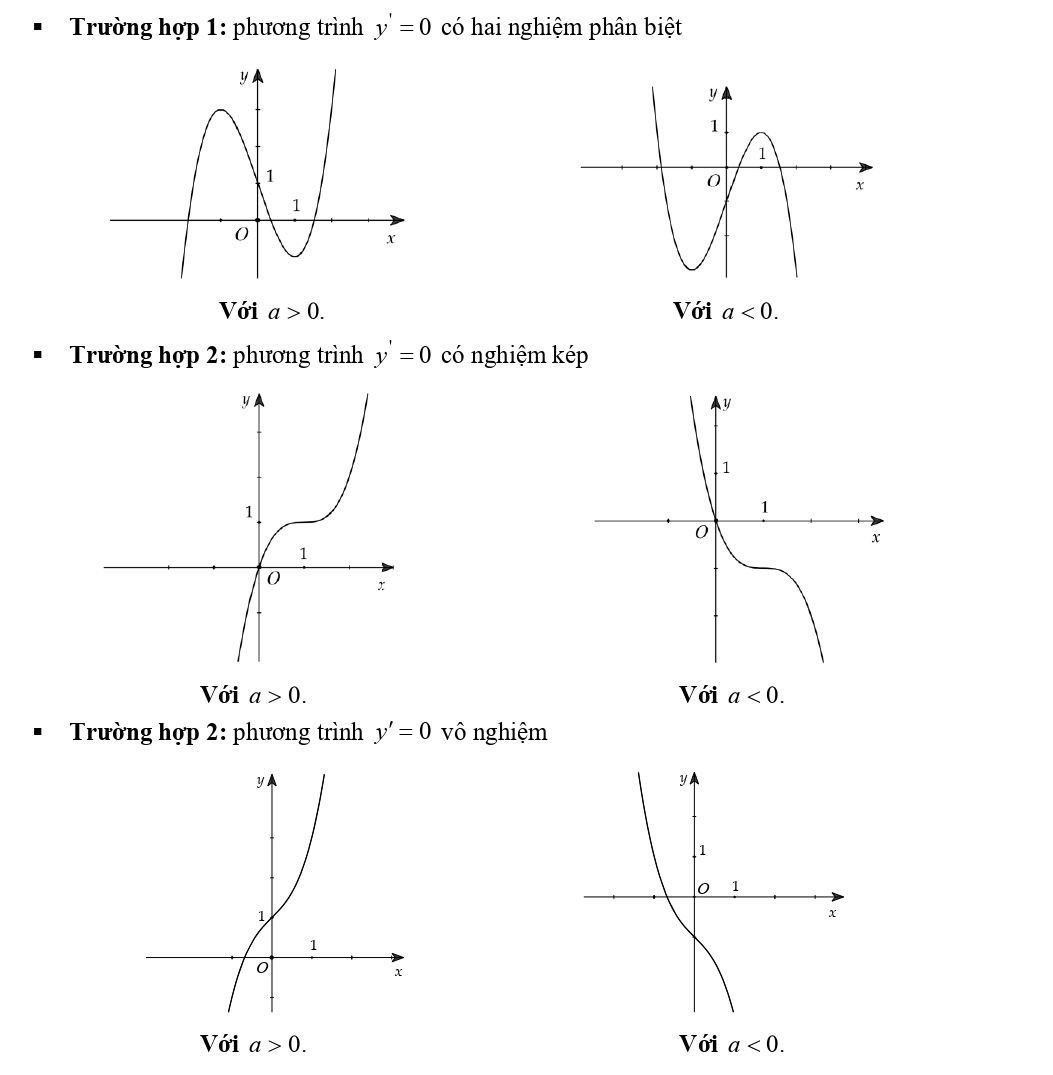
2. Hàm số trùng phương y = ax4 + bx2 + cx (a ≠ 0)

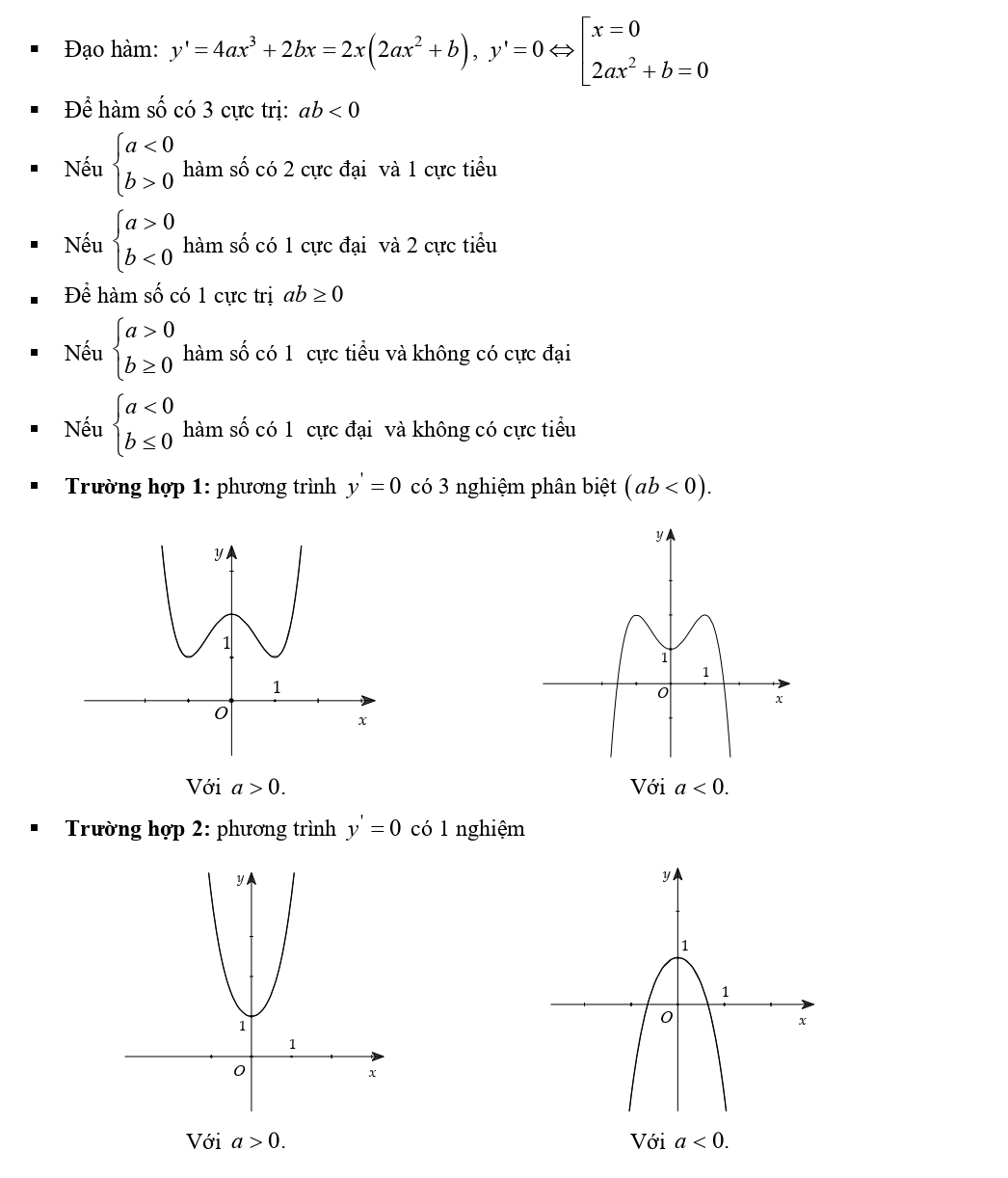
3. Hàm số bậc nhất y = (ax + b) / (cx + d), (c ≠ 0, ad - bc ≠ 0)

Xem thêm: Chuyên đề số phức ôn thi THPT Quốc Gia môn Toán

Tương giao đồ thị hàm số

1. Tọa độ giao điểm của hai đồ thị hàm số:

Phương pháp tính:

Cho 2 hàm số y = f(x), y = g(x) có đồ thị lần lượt là (C) và (C)'.

1. Lập phương trình hoành độ giao điểm của (C) và (C)': f(x) = g(x) (*)

2. Giải phương trình tìm x từ đó suy ra y và tọa độ giao điểm.

3. Số nghiệm của (*) là số giao điểm của (C) và (C)' . 

2. Tương giao của đồ thị hàm bậc ba

Phương pháp 1 - Bảng biến thiên (phương pháp đồ thị):

1. Lập phương trình hoành độ giao điểm dạng F(x,m) = 0 (phương trình ẩn x tham số m)

2. Cô lập m đưa phương trình về dạng m = f(x)

3. Lập bảng biến thiên cho hàm số y = f(x)

4. Dựa và giả thiết và bảng biến thiên từ đó suy ra m

=> Dấu hiệu: Sử dụng phương pháp bảng biến thiên khi m độc lập với x.

Phương pháp 2 - Nhẩm nghiệm, tam thức bậc 2:

Phương pháp 3 - Cực trị:

=> Dấu hiệu: Khi bài toán không cô lập được m và cũng không nhẩm được nghiệm.

Quy tắc:

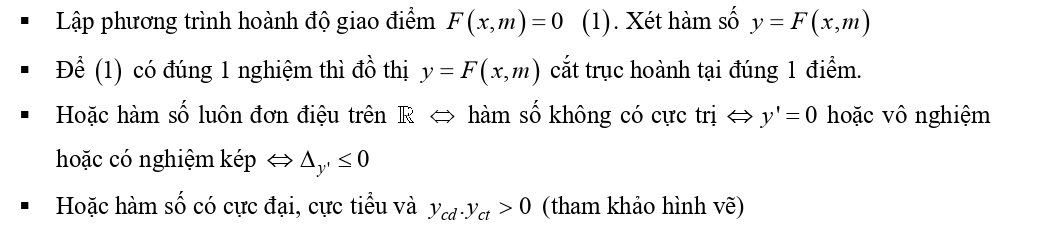
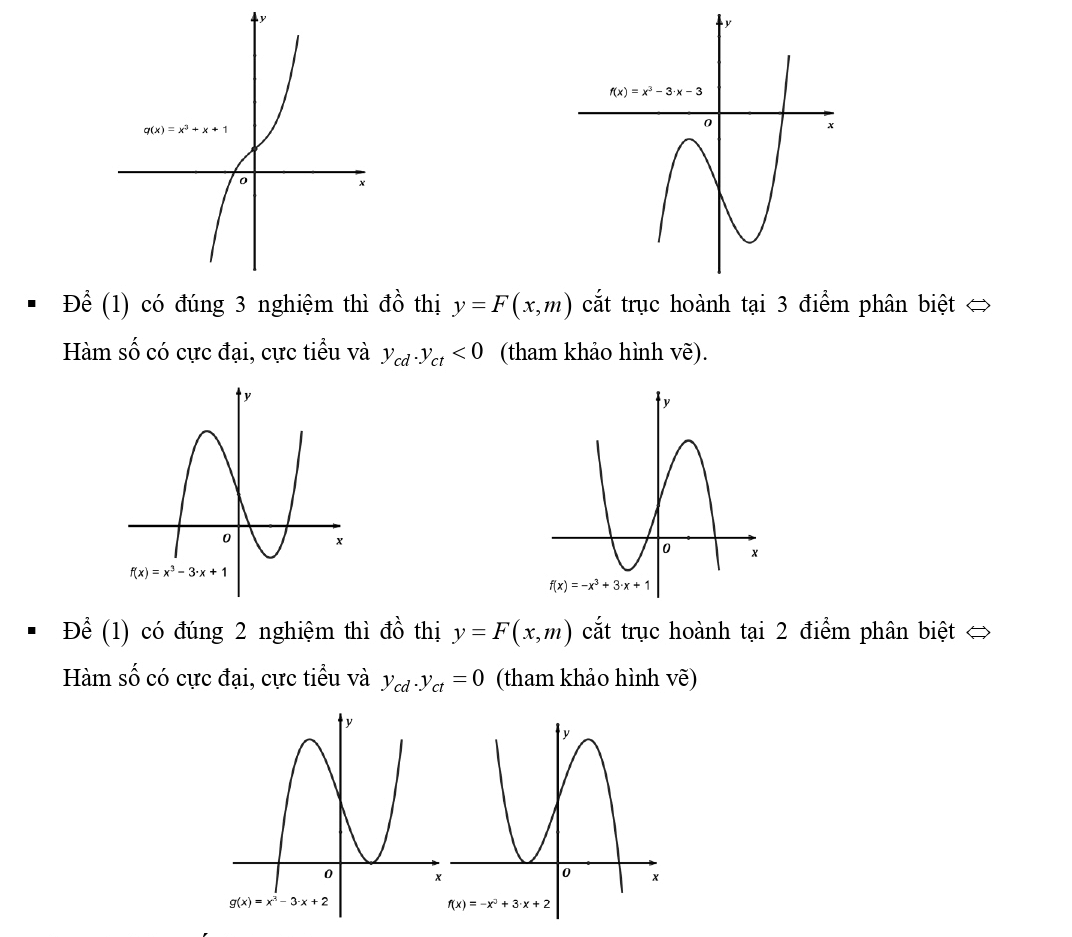
3. Tương giao của hàm số phân thức

Quy tắc:

• Tìm điều kiện tồn tại A, B ⇔ (1) có 2 nghiệm phân biệt.

• Xác định tọa độ của A và B.

• Dựa vào giả thiết xác lập phương trình ẩn m. Từ đó suy ra m

Công thức khoảng cách: 

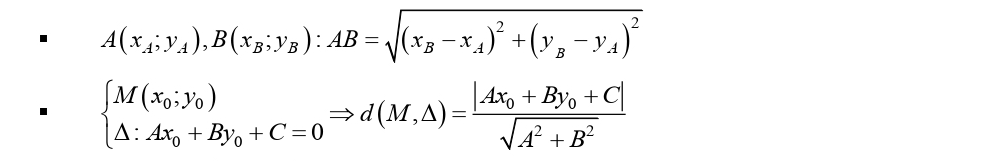
4. Tương giao của hàm số bậc bốn

Nghiệm của phương trình bậc bốn trùng phương ax4 + bx2 + cx = 0 (1)

Các dạng toán về tương giao đồ thị hàm số có thể xuất hiện trong đề thi THPT Quốc Gia, bao gồm:

• Dạng 1: Tương giao đồ thị hàm số không chứa tham số

• Dạng 2: Tương giao đồ thị hàm hợp không chứa tham số

• Dạng 3: Tương giao đồ thị hàm hợp có chứa tham số

• Dạng 4: Tương giao đồ thị hàm số có chứa giá trị tuyệt đối

• Dạng 5: Tương giao đồ thị hàm số bậc ba

• Dạng 6: Tương giao hàm trùng phương và một số bài toán khác

Tiếp tuyến của đồ thị hàm số

Tóm tắt lý thuyết về tiếp tuyến của đồ thị hàm số:

1. Viết phương trình tiếp tuyến tại điểm M (x0;y0) thuộc đồ thị hàm số

Cho hàm số (C): y = f(x) và điểm M (x0;y0) ∈ (C). Viết phương trình tiếp tuyến với đường cong (C) tại điểm M.

• Bước 1: Tính đạo hàm f’(x). Tìm hệ số góc của tiếp tuyến là f’(x0).

• Bước 2: Phương trình tiếp tuyến tại điểm M là: y = f’(x)(x - x0) + y0.

2. Viết phương trình tiếp tuyến có hệ số góc k cho trước

Gọi (∆) là tiếp tuyến cần tìm có hệ số góc k. 

Giả sử M (x0;y0) là tiếp điểm. Khi đó x0 thỏa mãn: f’(x0) = k (1).

Giải (1) tìm x0. Suy ra y = f(x0).

Phương trình tiếp tuyến cần tìm là: y = k(x - x0) + y0.

3. Điều kiện để hai hàm số tiếp xúc

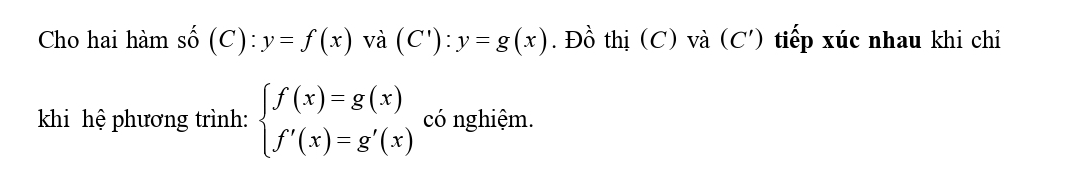
Với những kiến thức chuyên đề hàm số đầy đủ và hệ thống bài tập được phân loại khoa học trong bài viết này, hy vọng các bạn sẽ tự tin chinh phục mọi dạng bài chuyên đề hàm số trong kỳ thi THPT Quốc Gia sắp tới.