.png)
Bạn có bao giờ tự hỏi về sự quan trọng của chu vi hình thang cân trong cuộc sống hàng ngày? Trong bài viết này, Monkey sẽ cung cấp cho bạn một cái nhìn sâu hơn vào khái niệm này, cùng với công thức tính và cách áp dụng nó vào các bài tập ví dụ thực tế. Chu vi hình thang cân không chỉ là một đề tài toán học trừu tượng, mà còn có ứng dụng rất rộng rãi trong nhiều lĩnh vực. Hãy cùng khám phá những kiến thức thú vị ngay trong bài viết này nhé!
- Lộ trình Tiếng Anh toàn diện cho trẻ 0-11 tuổi chuẩn đầu ra Cambridge
- Áp dụng các phương pháp giáo dục được kiểm chứng trên thế giới
- Công nghệ M-Speak độc quyền chấm điểm và nhận xét phát âm chuẩn tới từng âm vị
- Kho học liệu khổng lồ với 4000+ hoạt động tương tác
- Hệ thống lớp học, giáo viên đồng hành cùng ba mẹ và bé
- Luyện đọc với kho 1000+ truyện tranh tương tác
- Rèn luyện kỹ năng Đọc - Hiểu thông qua trò chơi và câu hỏi tương tác
- Lộ trình học 14 cấp độ giúp dễ dàng nhận thấy sự tiến bộ của trẻ
- Công nghệ trí tuệ nhân tạo M-Speak chấm điểm và nhận xét phát âm khi bé kể chuyện
- 4 cấp độ học từ dễ đến nâng cao phù hợp với nhiều lứa tuổi & trình độ của trẻ
- Hệ thống bài học đồ sộ và bài bản giúp trẻ tự tin tiếp cận kiến thức mới
- Sách bài tập bổ trợ Monkey Math Workbook hỗ trợ đắc lực trong việc nâng cao năng lực toán học cho trẻ
- Hơn 60 chủ đề thuộc 7 chuyên đề toán học lớn giúp trẻ dễ dàng nắm bắt các khái niệm toán học
- Phát triển đồng bộ tư duy & ngôn ngữ giúp con học giỏi cả toán và tiếng Anh
- Áp dụng phương pháp học tập hiện đại qua trò chơi, hình ảnh, âm thanh
- Học vần chuẩn và nhanh nhất theo chương trình học vần theo sách giáo khoa mới
- Trẻ có thể đọc trôi chảy trước khi vào lớp 1 nhờ 700+ truyện tranh tương tác, 300+ sách nói
- Tăng khả năng Đọc - Hiểu với 1500+ câu hỏi tương tác sau truyện
- Phát triển trí tuệ cảm xúc (EQ) và nuôi dưỡng tâm hồn của trẻ nhờ 1000+ truyện cổ tích dân gian, thơ, bài học cuộc sống chọn lọc
- Hệ thống bài học đồ sộ, bài bản
- Trẻ tự tin tiếp thu kiến thức mới trên lớp
- Cấp độ học từ Dễ đến Nâng cao phù hợp với trình độ và nhận thức của trẻ
Ôn tập lý thuyết hình thang cân
Trước khi đi sâu vào công thức tính chu vi hình thang cân, chúng ta hãy cùng ôn tập là một số lý thuyết về hình thang cân mà học sinh cần phải ghi nhớ.
Hình thang cân là gì?
Hình thang là gì? Hình thang là tứ giác có một cặp cạnh song song và hai cặp cạnh còn lại không song song. Trong đó, các trường hợp đặc biệt của hình thang bao gồm: Hình thang cân, hình thang vuông, hình bình hành, hình chữ nhật,...
Hình thang cân là gì? Hình thang cân chính là một dạng hình thang đặc biệt có hai góc kề một đáy bằng nhau. (Như hình minh họa)
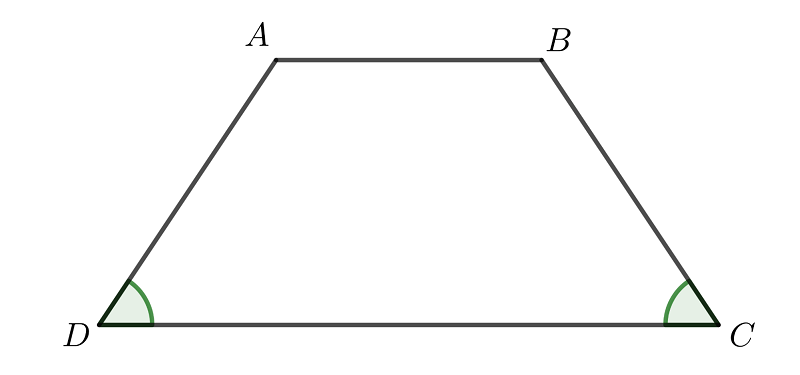
Tính chất của hình thang cân
Dưới đây là một số tính chất của hình thang cân mà bạn cần ghi nhớ:
-
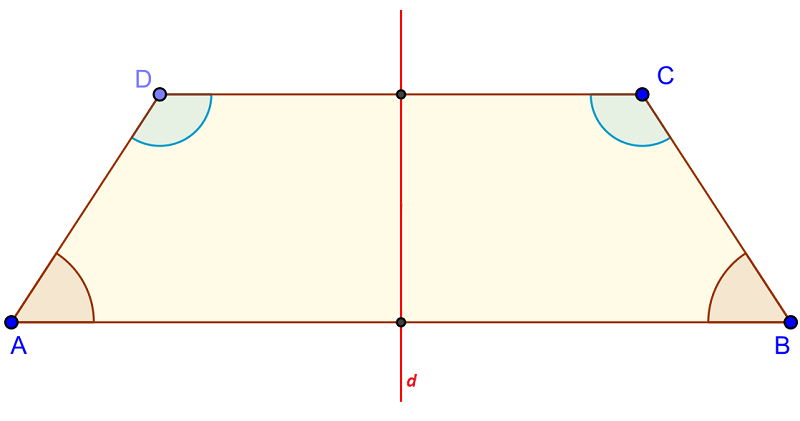
Hai cạnh bên của hình thang cân bằng nhau.
-
Hai đường chéo của hình thang cân cũng bằng nhau.
-
Hai góc kề một đáy của hình thang cân có giá trị bằng nhau.
-
Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm của hai cạnh đáy.
Cần lưu ý rằng, một hình thang có hai cạnh bên bằng nhau chưa chắc đã là hình thang cân, vì hình thang cân còn phải xem xét các dấu hiệu khác, được trình bày ngay dưới đây.
|
ĐỪNG BỎ LỠ!! Chương trình học Toán bằng tiếng Anh, giúp phát triển tư duy một cách toàn diện nhất. Nhận ưu đãi lên đến 40% NGAY TẠI ĐÂY! |
Dấu hiệu nhận biết hình thang cân
Hai dấu hiệu cụ thể để nhận biết một hình thang cân:
-
Dấu hiệu 1 - Hai góc kề một đáy bằng nhau: Một hình thang được coi là cân khi có hai góc ở hai bên của đáy mà góc này có giá trị bằng nhau. Điều này có nghĩa là khi bạn đo góc tạo bởi đáy và một cạnh bên, rồi đo góc tạo bởi đáy và cạnh bên còn lại, hai góc này sẽ có giá trị giống nhau.
-
Dấu hiệu 2 - Hai đường chéo bằng nhau: Một hình thang cân là khi có hai đường chéo có độ dài bằng nhau. Điều này có nghĩa rằng đoạn thẳng nối hai đỉnh không kề nhau của hình thang cân có cùng độ dài.
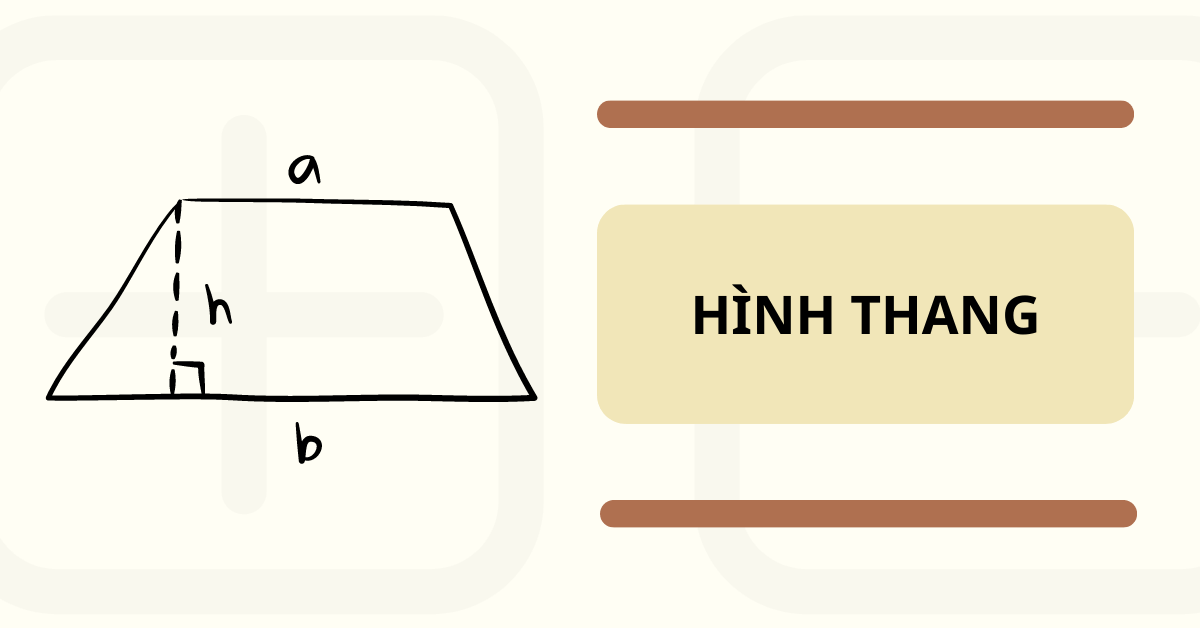
Công thức tính chu vi hình thang cân
Chu vi hình thang cân là tổng độ dài của hai cạnh đáy và hai cạnh bên.
Để tính chu vi của một hình thang cân, bạn có thể sử dụng công thức sau:
P = a + b + (2 x c)
Trong đó:
-
P là chu vi hình thang cân.
-
a và b là độ dài hai cạnh đáy.
-
c là độ dài cạnh bên.
Ví dụ:
Cho hình thang cân ABCD, có AB = 10cm, CD = 15cm, cạnh bên BC = 8cm. Tính chu vi hình thang ABCD.
Giải:
Theo công thức tính chu vi hình thang cân, ta có:
P = 10 + 15 + (2 x 8) = 41 cm
Chu vi hình thang ABCD là 41 cm.
Lưu ý: Công thức tính chu vi hình thang cân cũng có thể áp dụng cho hình thang thường.
Bên cạnh công thức tính chu vi hình thang cân, thì bạn cũng cần ghi nhớ một công thức khác cũng không kém phần quan trọng, đó là diện tích hình thang cân. Cụ thể như sau:
Diện tích hình thang cân bằng trung bình cộng hai đáy nhân với chiều cao.
Để tính diện tích của một hình thang cân, bạn có thể sử dụng công thức sau:
S = (a + b)/2 x h
Trong đó:
-
S là diện tích hình thang cân.
-
a và b là độ dài hai cạnh đáy.
-
h là chiều cao hình thang.
Ví dụ:
Cho hình thang cân ABCD, có AB = 10cm, CD = 15cm, chiều cao h = 8cm. Tính diện tích hình thang ABCD.
Giải:
Theo công thức tính diện tích hình thang cân, ta có:
S = (10 + 15)/2 x 8 = 100 cm2
Diện tích hình thang ABCD là 100 cm2.
Lưu ý: Công thức tính diện tích hình thang cân cũng có thể áp dụng cho hình thang thường.
Hình thang cân: Khái niệm, tính chất, dấu hiệu nhận biết & các công thức tính
Hình thang là gì? Tính chất, dấu hiệu nhận biết hình thang
Công thức tính diện tích hình thang vuông & bài tập có lời giải chi tiết
Các bài tập ví dụ về phép tính chu vi hình thang cân
Dưới đây là một số bài tập về phép tính chu vi hình thang cân:
Bài 1: Cho hình thang cân EFGH với EF = 12cm, GH = 14cm và cạnh bên EH = 7cm. Tính chu vi hình thang EFGH.
Giải:
Theo công thức tính chu vi hình thang cân, ta có:
P = 12 + 14 + (2 x 7) = 40 cm
Chu vi hình thang EFGH là 40 cm.
Bài 2: Cho hình thang cân IJKL với IJ = 20cm, KL = 25cm và cạnh bên IK = 15cm. Tính chu vi hình thang IJKL.
Giải:
Theo công thức tính chu vi hình thang cân, ta có:
P = 20 + 25 + (2 x 15) = 75 cm
Chu vi hình thang IJKL là 75 cm.
Bài 3: Hình thang cân có hai cạnh đáy lần lượt dài 8cm và 10cm, cạnh bên là 6cm. Tính chu vi của nó.
Giải:
Theo công thức tính chu vi hình thang cân, ta có:
P = 8 + 10 + (2 x 6) = 30 cm
Chu vi hình thang là 30 cm.
Bài 4: Cho hình thang cân với hai cạnh đáy dài 11cm và 13cm, cạnh bên dài 9cm. Tính chu vi của nó.
Giải:
Theo công thức tính chu vi hình thang cân, ta có:
P = 11 + 13 + (2 x 9) = 42 cm
Chu vi hình thang là 42 cm.
Bài 5: Hình thang cân có hai cạnh đáy là 5cm và 6cm, cạnh bên dài 4cm. Tính chu vi của nó.
Giải:
Theo công thức tính chu vi hình thang cân, ta có:
P = 5 + 6 + (2 x 4) = 19 cm
Chu vi hình thang là 19 cm.
Xem thêm:
- Monkey Math - Ứng dụng học toán bằng tiếng Anh số 1 cho trẻ mầm non & tiểu học
- Công thức tính chu vi hình thang thường, vuông, cân & cách giải đơn giản
Ứng dụng thực tiễn của chu vi hình thang cân
Chu vi của hình thang cân có nhiều ứng dụng thực tiễn quan trọng trong nhiều lĩnh vực khác nhau, cụ thể như:
-
Đo đạc, xây dựng: Chu vi hình thang cân được sử dụng để đo chiều dài của một công trình có dạng hình thang cân, chẳng hạn như mái nhà, sàn nhà,...
Ví dụ: Để đo chiều dài của mái nhà, người ta có thể dùng thước dây để đo chu vi của mái nhà. Sau đó, sử dụng công thức tính chu vi hình thang cân để tính ra chiều dài của mỗi cạnh của mái nhà.
-
Thiết kế đồ họa: Chu vi hình thang cân được sử dụng để thiết kế các vật dụng có dạng hình thang cân, chẳng hạn như túi xách, khăn trải bàn,..
Ví dụ: Để thiết kế một chiếc túi xách có dạng hình thang cân, người ta cần tính toán chu vi của túi xách để xác định kích thước của túi xách.
-
Thiết kế nội thất: Chu vi hình thang cân được sử dụng để thiết kế các đồ nội thất có dạng hình thang cân, chẳng hạn như kệ sách, bàn ghế,...
Ví dụ: Để thiết kế một chiếc kệ sách có dạng hình thang cân, người ta cần tính toán chu vi của kệ sách để xác định kích thước của kệ sách.
-
Thiết kế thời trang: Chu vi hình thang cân được sử dụng để thiết kế các trang phục có dạng hình thang cân, chẳng hạn như váy, áo,...
Ví dụ: Để thiết kế một chiếc váy có dạng hình thang cân, người ta cần tính toán chu vi của váy để xác định kích thước của váy.
Nhìn chung, chu vi hình thang cân là một kiến thức toán học quan trọng có nhiều ứng dụng thực tiễn trong cuộc sống. Hy vọng rằng, những thông tin mà Monkey cung cấp trên là là hữu ích với bạn. Hãy xem thêm các bài viết bổ ích khác tại chuyên mục Học Toán của chúng mình nhé!
