.png)
Hình thang cân là một trong những hình học cơ bản hiện nay. Để hiểu rõ hơn thế nào là hình thang cân, đặc điểm, tính chất, dấu hiệu nhận biết và các công thức tính chu vi, diện tích thì nội dung sau đây Monkey sẽ phân tích chi tiết.
- Khởi đầu tốt nhất cho con bắt đầu học tiếng Anh. Con học càng sớm càng có lợi thế.
- Tích lũy 1000+ từ vựng mỗi năm và 6000 mẫu câu tiếng Anh trước 10 tuổi.
- Linh hoạt sử dụng trên nhiều thiết bị.
- Thành thạo các kỹ năng tiếng Anh ngay trước 10 tuổi với hơn 1000 đầu truyện, hơn 100 bài học, 300+ sách nói. Nội dung thêm mới mỗi tuần.
- Hơn 1.000 đầu truyện, hơn 300 bài học, gần 300 sách nói - thêm mới mỗi tuần.
- Phát âm chuẩn ngay từ đầu nhờ Monkey Phonics - giúp đánh vần tiếng Anh dễ như tiếng Việt.
- Đánh vần chuẩn nhờ học phần Học Vần - cập nhật theo chương trình mới nhất của Bộ GD&ĐT.
- Đọc - hiểu, chính tả tiếng Việt dễ dàng và nhẹ nhàng hơn ngay tại nhà.
- Bồi dưỡng trí tuệ cảm xúc (EQ) nhờ hơn 450 câu chuyện thuộc 11 chủ đề, nhiều thể loại truyện.
Hình thang cân là gì?
Là một trong các loại hình học phổ biến, hình thang cân có những đặc điểm nổi bật sau đây:
Khái niệm hình thang cân
Hình thang cân là tứ giác đặc biệt có hai cạnh song song (hình thang) và có hai góc kề một cạnh đáy bằng nhau.
Ví dụ: ABCD là hình thang cân (đáy AB, CD) <=> AB // CD và góc C = góc D
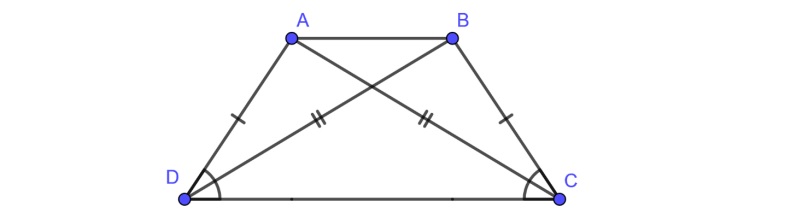
Đặc điểm tính chất hình thang cân
Là một tứ giác đặc biệt, nên hình thang cân có những tính chất như sau:
- Hình thang có hai cạnh bên bằng nhau
Ví dụ: ABCD là hình thang cân (đáy AB, CD) => AD = BC
- Hình thang có hai góc kề cạnh đáy bằng nhau
Ví dụ: ABCD là hình thang cân (đáy AB, CD) => AC = BD
- Hình thang có hai đường chéo bằng nhau
Ví dụ: ABCD là hình thang cân (đáy AB, CD) => góc C = góc D và góc A = góc B
Ngoài ra, hình thang cân nội tiếp đường tròn chính là hình có 4 điểm đều thuộc một hình tròn.
Dấu hiệu nhận biết hình thang cân
-
Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân.
-
Hình thang có hai đường chéo bằng nhau là hình thang cân.
-
Hình thang nội tiếp đường tròn là hình thang cân.
Ví dụ: Trong các tứ giác ABCD và EFGH trên giấy kẻ ô vuông ở hình sau, tứ giác nào là hình thang cân? Vì sao?
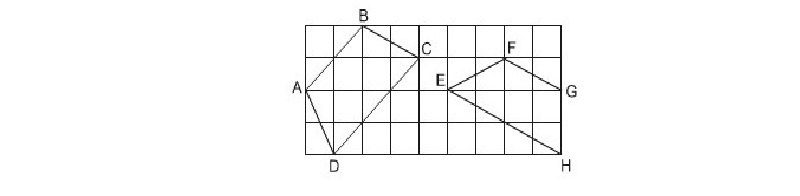
Hướng dẫn giải:
Để biết được đâu là hình thang cân, ta sẽ dựa vào tính chất của hình để xem xét. Cụ thể, nhìn vào hình được vẽ trên các ô vuông nên sẽ dễ dàng nhận biết được độ dài các cạnh bên.
Theo đó: Trong 2 hình trên, tứ giác ABCD là hình thang cân. Bởi vì AD = BC (hai đường chéo của 2 hình tam giác với độ dài cạnh bằng nhau). Còn tứ giác EFGH không phải là hình thang cân, vì chúng ta nhìn 2 cạnh EF > GH.
* Lưu ý: Hình thang cân sẽ có 2 cạnh bên bằng nhau, nhưng điều ngược lại chưa hẳn đã đúng. Chẳng hạn tứ giác có 2 cặp cạnh song song, cùng cạnh bên bằng nhau nhưng đó không phải là hình thang cân.
Cách chứng minh hình thang cân
Để có thể chứng minh được một hình thang là hình thang cân, ta dựa vào đặc điểm sau:
-
Chứng minh hình thang có hai góc kề một đáy bằng nhau => hình thang đó là hình thang cân.
-
Chứng minh hình thang có hai đường chéo bằng nhau => hình thang đó là hình thang cân.
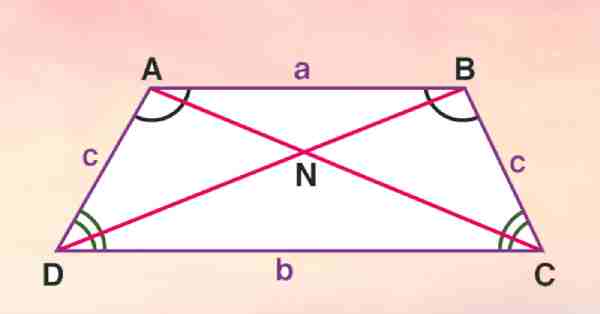
Công thức tính diện tích và chu vi hình thang cân
Cũng tương tự như các hình học khác, với hình thang cân cũng sẽ có những công thức về tính chu vi và diện tích cơ bản sau đây:
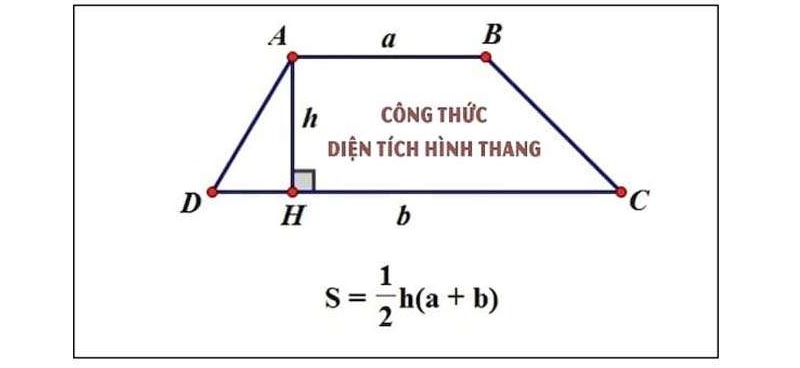
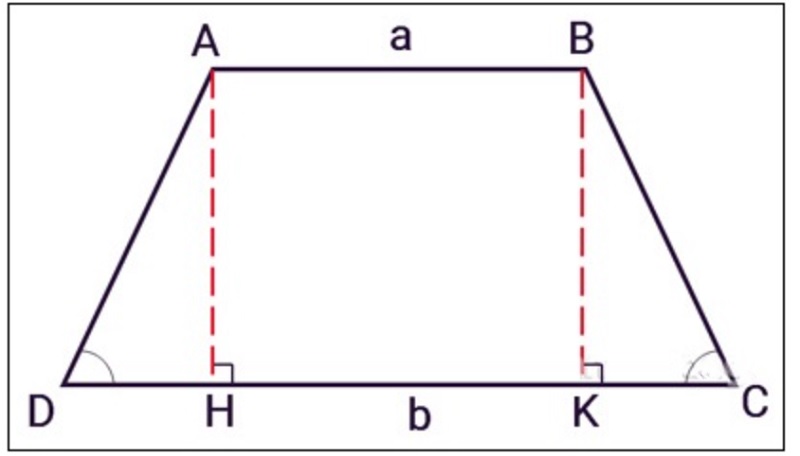
Công thức tính diện tích hình thang cân
Cách tính diện tích hình thang cân cũng sẽ áp dụng như công thức tính diện tích hình thang thông thường, sẽ bằng chiều cao nhân với trung bình cộng hai đáy.
* Lưu ý: Chiều cao ở đây chính là cạnh bên vuông góc với cả 2 đáy.
| Công thức: S = (a + b)/2 x h |
Trong đó:
-
S là diện tích hình thang.
-
a và b là độ dài 2 cạnh đáy.
-
h là độ dài cạnh bên vuông góc với 2 đáy.
Công thức tính chu vi hình thang cân
Chẳng hạn, cho hình thang ABCD cân với độ dài 2 cạnh đáy tương ứng là a và b, độ dài cạnh bên là c. Lúc này, công thức tính chu vi hình thang cân ABCD sẽ là:
| P = a + b + 2c |
Một số dạng bài tập về hình thang cân thường gặp
Khi mới làm quen với kiến thức về hình thang cân, các em thường sẽ được gặp một số dạng toán quen thuộc sau đây:
Dạng 1: Tính chu vi hình bình thang khi biết độ dài các đáy và cạnh bên
Ví dụ: Cho hình thang ABCD cân, biết đáy lớn bằng 12 cm; đáy bé bằng 10 cm và hai cạnh bên lần lượt bằng 7 cm và 8 cm. Tính chu vi hình thang ABCD.
Hướng dẫn giải:
Chu vi hình thang ABCD cân là:
12 + 10 + 7 + 8 = 37 (cm)
Đáp số: 37cm
Dạng 2: Tính độ dài cạnh bên của hình thang cân khi biết chu vi
Ví dụ: Cho hình thang ABCD cân có hai cạnh bên bằng nhau biết chu vi của hình thang bằng 68cm và độ dài hai cạnh đáy lần lượt là 20cm và 26cm. Tính độ dài của hình thang ABCD cân.
Hướng dẫn giải:
Tổng độ dài hai cạnh bên của hình thang ABCD là:
68 – 20 – 26 = 22 (cm)
Độ dài cạnh bên của hình thang là:
22 : 2 = 11 (cm)
Đáp số: 11cm
Dạng 3: Tính diện tích hình thang cân khi biết độ dài hai đáy và chiều cao
Ví dụ: Cho hình thang ABCD cân, biết độ dài đáy nhỏ bằng 5cm, đáy lớn bằng 10cm. Chiều cao của hình thang bằng 6cm. Tính diện tích của hình thang ABCD.
Hướng dẫn giải:
Diện tích hình thang ABCD là:
(5 + 10) x 6 : 2 = 45 (cm2)
Đáp số: 45cm2
Dạng 4: Tính chiều cao khi biết độ dài hai đáy và diện tích hình thang cân
Ví dụ: Cho hình thang ABCD có diện tích bằng 14dm2, đáy bé bằng 2dm và đáy lớn bằng 5dm. Tính độ dài chiều cao của hình thang đó.
Từ công thức tính diện tích của hình thang, ta tìm được cách tính chiều cao của hình tương ứng bằng cách ta lấy diện tích chia cho trung bình cộng của hai đáy. Tương ứng h = S x 2 : (a + b)
Hướng dẫn giải:
Độ dài chiều cao của hình thang là:
14 x 2 : (2 + 5) = 4 (dm)
Đáp số: 4dm
Dạng 5: Tính diện tích hình thang cân khi chưa biết độ dài hai đáy và chiều cao
Ví dụ: Cho hình thang ABCD cân chiều cao bằng 56cm. Đáy lớn hơn đáy bé 24cm và đáy bé bằng 2/5 đáy lớn. Tính diện tích hình thang ABCD.
Hướng dẫn giải:
Hiệu số phần bằng nhau là:
5 – 2 = 3 (phần)
Độ dài đáy lớn là:
24 : 3 x 5 = 40 (cm)
Độ dài đáy bé là:
40 – 24 = 16 (cm)
Diện tích hình thang là:
(16 + 40) x 56 : 2 = 1568 (cm2)
Đáp số: 1568cm2
Ứng dụng của hình thang cân trong thực tế
Hình thang cân là một hình học khá quen thuộc và phổ biến. Ngoài được ứng dụng trong toán học, nó cũng được dùng làm đồ chơi cho trẻ em với hình dạng tương ứng, hay các mô hình bằng nhựa để học tập và vui chơi, các đồ dùng như bàn ghế, kệ sách…
Các bài toán liên quan đến hình thang cân trong SGK kèm đáp án
Đối với kiến thức về hình thang cân, thường các em sẽ bắt đầu được học từ chương trình toán lớp 8. Vậy nên, dưới đây Monkey sẽ tổng hợp một số bài tập toán trong SGK toán lớp 8 về hình thang cân kèm đáp án để các em tham khảo thêm:
Bài tập thực hành để rèn kỹ năng
Ngoài bài tập trong SGK, Monkey sẽ tổng hợp thêm một số bài tập về hình thang cân để các em có thể áp dụng kiến thức đã học để chinh phục hiệu quả:
Kinh nghiệm học toán hình thang cân hiệu quả
Để giúp các em học hiểu và dễ chinh phục các bài tập về hình thang cân, dưới đây là một số bí quyết mà Monkey tổng hợp để bé tham khảo thêm.
Trang bị nền tảng và niềm yêu thích toán học cùng Monkey Math
Monkey Math là ứng dụng dạy học toán online dành cho trẻ em đang được nhiều phụ huynh tin tưởng lựa chọn hiện nay, với nội dung dạy học bám sát chương trình GDPT mới nhất của Bộ đưa ra, để không chỉ trang bị nền tảng toán học trong đời sống mà còn hỗ trợ việc học trên lớp tốt nhất.
Chính vì vậy, Monkey Math sẽ không giảng dạy theo hướng truyền thụ kiến thức như cách truyền thống. Thay vào đó, ứng dụng sẽ áp dụng đa phương pháp dạy học tích cực thông qua trò chơi, sách bài tập bổ trợ, các hoạt động toán học… Kết hợp cùng với âm thanh sống động, hình ảnh đồ hoạ sinh động giúp tăng khả năng tiếp thu và sự hứng thú hơn khi bé học toán hơn.
Đồng thời, nội dung bài học trên ứng dụng đa dạng với nhiều chủ đề thuộc nhiều chuyên đề từ đại số đến hình học, bao gồm cả kiến thức về hình thang cân. Tất cả được sắp xếp và cá nhân hoá theo từng đối tượng, phân chia thành các cấp độ từ dễ đến khó để ba mẹ dễ dàng lựa chọn bài học phù hợp với năng lực của trẻ nhất.
Để hiểu rõ hơn về các phương pháp dạy tại Monkey Math, ba mẹ có thể tham khảo qua video sau hoặc đăng ký để được tư vấn chu đáo:
Ghi nhớ các công thức hình thang cân qua thơ ca
Đối với các em nhỏ, việc ghi nhớ bài thơ hay bài hát thường sẽ dễ dàng hơn so với một đoạn văn. Vậy nên, để giúp việc tính toán dễ nhớ, dễ hiểu hơn thì ba mẹ có thể sáng tạo hoặc sưu tầm những bài thơ liên quan tới các công thức về hình thang cân. Chẳng hạn như:
“ Muốn tính diện tích hình thang
Đáy lớn, đáy bé ta đem cộng vào
Cộng vào nhân với chiều cao
Chia đôi kết quả thế nào cũng ra”
Luyện tập, thực hành thường xuyên
Để phòng tránh trường hợp bé “học trước quên sau”, ba mẹ nên khích lệ, yêu cầu bé luyện tập, thực hành thường xuyên. Từ việc làm bài tập trong SGK, tham khảo thêm nhiều kiến thức mới trên internet, luyện đề thi, tổ chức các trò chơi hay cuộc thi nhỏ về toán học…
Bên cạnh đó, ba mẹ cũng nên thường xuyên kiểm tra kiến thức của con, để biết con đang gặp khó khăn phần nào, có cần hỗ trợ gì không?... Chính điều này sẽ góp phần thúc đẩy khả năng tư duy, hứng thú và tiếp thu kiến thức của bé khi học toán tốt hơn, bớt nhàm chán hơn.
Kết luận
Trên đây là những thông tin kiến thức cơ bản về hình thang cân, một hình học đặc biệt sẽ thường xuất hiện trong đề thi mà các em cần nắm rõ. Nếu ba mẹ không có nhiều thời gian và kinh nghiệm trong việc dạy bé học toán thì có thể tham khảo ứng dụng Monkey Math để hỗ trợ xây dựng nền tảng toán học cho bé tốt hơn nhé.
.jpg)
