Cách tính diện tích hình thang lớp 5 & bài tập có cách giải chi tiết

Ôn tập kiến thức về hình thang lớp 5

Hình thang là một trong những hình từ giác đặc biệt với những đặc điểm nổi trội sau đây:

Định nghĩa về hình thang

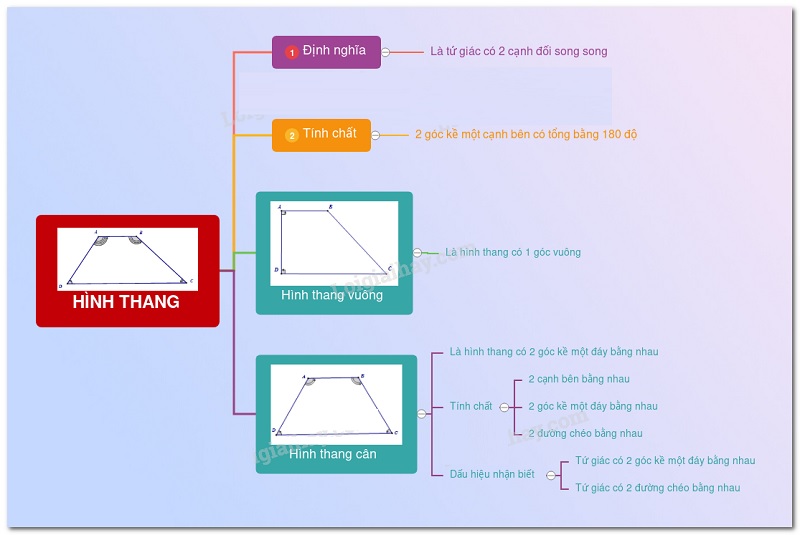
Hình thang là một hình học Euclide, là hình tứ giác có 2 cạnh đối song song hay còn gọi là các cạnh đáy của hình, còn 2 cạnh hai bên được gọi là cạnh bên.

Hay hình thang là hình tứ giác với 2 cạnh đối song song, 2 góc kề một cạnh bên sẽ có tổng số đo góc bằng 180 độ.

Hình thang là tứ giác lồi có 4 cạnh. Trong đó, hai cạnh song song với nhau được gọi là cạnh đáy, hai cạnh còn lại được gọi là hai cạnh bên.

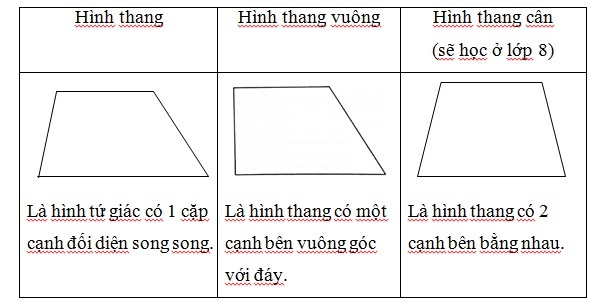
Bên cạnh đó, hình thang còn được chia thành một số trường hợp đặc biệt khác như:

• Hình thang vuông: Hình thang có 1 góc vuông được gọi là hình thang vuông

• Hình thang cân: Hình thang có 2 góc kề một cạnh đáy bằng nhau là hình thang cân.

• Hình thang vuông cân: Là hình thang vừa vuông vừa cân và còn được gọi là hình chữ nhật.

Tính chất của hình thang

Là một dạng hình học đặc biệt, nên hình thang có những tính chất cơ bản như:

Tính chất về cạnh:

• Hình thang có 2 cạnh đáy bằng nhau thì hai cạnh bên bằng nhau và song song.

• Hình thang có 2 cạnh bên song song thì chúng bằng nhau và hai cạnh đáy cũng bằng nhau.

Đường trung bình của hình thang

Đường trung bình của hình thang chính là đoạn thẳng nối trung điểm của 2 cạnh bên hình thang.

Tính chất: Đường trung bình của hình thang sẽ song song với hai đáy và bằng nửa tổng hai đáy.

Tính chất về góc

Hình thang có hai góc kề một cạnh bên sẽ có tổng số đo bằng 180 độ ( Hai góc nằm ở vị trí trong cùng của hai đoạn thẳng song song là hai cạnh đáy) .

Trong đó, với hình thang cân sẽ có hai góc kề một đáy bằng nhau.

Dấu hiệu nhận biết hình thang

Dựa vào định nghĩa cũng có thể thể suy ra được dấu hiệu nhận biết của hình thang. Điển hình nhất là tứ giác có hai cạnh đối song song với nhau.

Ví dụ: Tứ giác ABCD có AB // CD ⇔ Tứ giác ABCD là hình thang.

Ngoài ra, dưới đây cũng là một số dấu hiệu nhận biết cơ bản của hình thang để mọi người tham khảo.

• Hình thang là hình tứ giác có hai cạnh đối song song với nhau.

• Tứ giác là hình thang có một góc vuông là hình thang vuông.

• Tứ giác là hình thang có hai góc kề 1 cạnh đáy bằng nhau thì là hình thang cân.

• Tứ giác là hình thang có hai cạnh bên hình thang bằng nhau thì là hình thang cân.

• Tứ giác là hình thang mà hai đường chéo của chúng bằng nhau thì là hình thang cân.

Trong đó, dấu hiệu nhận biết của hình thang cân sẽ đơn giản hơn như sau:

• Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân.

• Hình thang có hai đường chéo bằng nhau là hình thang cân.

• Hình thang có hai trục đối xứng của hai đáy trùng nhau là hình thang cân.

• Hình thang có hai cạnh bên bằng nhau là hình thang cân.

• Hình thang nội tiếp đường tròn là hình thang cân

Công thức tính diện tích hình thang lớp 5

Công thức tính diện tích hình thang sẽ bằng trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy.

Cụ thể:

S = (a + b)/2 x h

Trong đó: 

• S là diện tích hình thang.

• a và b là độ dài 2 cạnh đáy.

• h là chiều cao hạ từ cạnh đáy a xuống b hoặc ngược lại (khoảng cách giữa 2 cạnh đáy).

Các bài viết không thể bỏ lỡ

Cách giải các dạng toán lớp 5 hình học từ cơ bản đến nâng cao

Hai đường thẳng vuông góc: Khái niệm, đặc điểm, bài tập và cách giải chi tiết

Tổng hợp các dạng toán về hình chữ nhật lớp 5 từ cơ bản đến nâng cao

Các dạng bài tập tính diện tích hình thang toán lớp 5

Trong chương trình toán lớp 5, các em sẽ được làm quen một số dạng toán cơ bản về cách tính diện tích hình thang như sau:

Dạng 1: Tính diện tích hình bình thang khi biết độ dài hai đáy và chiều cao

Phương pháp giải: Các em sẽ dựa vào công thức chuẩn của cách tính diện tích hình thang “bằng trung bình cộng 2 cạnh đáy nhân với chiều cao giữa 2 đáy” để từ đó tính được diện tích theo số liệu bài toán đã cho.

Ví dụ: Cho hình thang có độ dài đáy nhỏ bằng 7cm, đáy lớn bằng 14cm. Chiều cao của hình thang bằng 12cm. Tính diện tích của hình thang đó.

Lời giải:

Diện tích hình thang là:

(7 + 14) x 12 : 2 = 126 (cm2)

Đáp số: 126cm2

Dạng 2: Tính chiều cao khi biết độ dài hai đáy và diện tích

Phương pháp giải: Nếu đề bài cho số liệu diện tích và độ dài hai đáy, yêu cầu tính chiều cao thì từ công thức tính diện tích hình thang, ta sẽ suy luận được công thức tính chiều cao tương ứng là h = S x 2 : (a + b).

Ví dụ: Một hình thang vuông có diện tích bằng 14dm2, đáy bé bằng 2dm và đáy lớn bằng 5dm. Tính độ dài chiều cao của hình thang vuông đó.

Hướng dẫn giải:

Độ dài chiều cao của hình thang là:

14 x 2 : (2 + 5) = 4 (dm)

Đáp số: 4dm

Dạng 3: Tính diện tích hình thang khi chưa biết độ dài hai đáy và chiều cao

Phương pháp giải: Đây là dạng toán nâng cao hơn, đòi hỏi các em cần phải dựa vào số liệu đã cho để tìm được chiều cao và độ dài hai đáy tương ứng, từ đó mới áp dụng công thức để tính được diện tích của hình thang.

Ví dụ: Một hình thang có chiều cao bằng 56cm. Đáy lớn hơn đáy bé 24cm và đáy bé bằng 2/5 đáy lớn. Tính diện tích hình thang.

Hướng dẫn giải:

Hiệu số phần bằng nhau là:

5 – 2 = 3 (phần)

Độ dài đáy lớn là:

24 : 3 x 5 = 40 (cm)

Độ dài đáy bé là:

40 – 24 = 16 (cm)

Diện tích hình thang là:

(16 + 40) x 56 : 2 = 1568 (cm2)

Đáp số: 1568cm2

Đáp án bài tập diện tích hình thang lớp 5 (SGK)

Trong chương trình toán lớp 5 của SGK hiện hành, bé sẽ được làm quen với một số bài tập tại trang 93 như sau:

Câu 1: Tính diện tích hình thang biết

a) Độ dài hai đáy lần lượt là 12 cm và 8 cm; chiều cao là 5 cm.

b) Độ dài hai đáy lần lượt là 9,4 m va 6,6m; chiều cao là 10,5 m

Hướng dẫn: 

Áp dụng công thức S= ((a+b) × h) : 2 ta tính được:

a. ((a+b) × h) : 2=((12+8) × 5) : 2=50 (cm2)

b. ((9.4 + 6.6) x 10.5) : 2 = 84 (cm2)

Đáp số : a) 50cm2, b) 84cm2

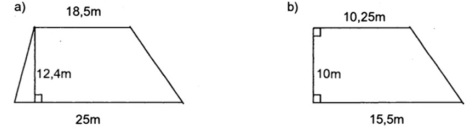
Câu 2: Tính diện tích mỗi hình thang sau:

Lời giải

a, Diện tích hình thang là: (18,5 + 25) x 12,4 : 2 = 269,7m²

b, Diện tích hình thang là: (10,25 + 15,5) x 10 : 2 = 128,75m²

Câu 3: Một thửa ruộng hình thang có độ dài hai đáy lần lượt là 110m và 90,2m. Chiều cao bằng trung bình cộng của hai đáy. Tính diện tích thửa ruộng đó.

Lời giải:

Chiều cao của thửa ruộng là:

(110+90,2)2=100,1(m)

Diện tích thửa ruộng  là:

S = ((a+b)×h)) /2= ((110+90,2) × 100,1) / 2 = (200,2 × 100,1) / 2=10000,01  (m2)

Câu 4: Hình thang có tổng độ dài hai đáy bằng 24 cm, đáy lớn hơn đáy bé 1,2 cm, chiều cao kém đáy bé 2,4 cm. Tính diện tích hình thang.

Lời giải

Đáy bé là: (24 – 1,2) : 2 = 11,4cm

Chiều cao của hình thang là: 11,4 – 2,4 = 9cm

Diện tích của hình thang là: 24 x 9 : 2 = 108m²

Câu 5: Một thửa ruộng hình thang có đáy lớn 120 m, đáy bé bằng 2/3 đáy lớn và bằng 4/3 chiều cao. Người ta trồng ngô trên thửa ruộng đó, tính ra trung bình 100 m2 thu được 50 kg ngô. Hỏi cả thửa ruộng thu được bao nhiêu tạ ngô?

Lời giải

Đáy bé là: 120 x 2 : 3 = 80m

Chiều cao là: 80 x 3 : 4 = 60m

Diện tích của thửa ruộng hình thang là: (120 + 80) x 60 : 2 = 6000m²

Số kg ngô thu được là: 6000 : 50 = 120kg

Đổi 120kg = 1,2 tạ

Câu 6: Thửa ruộng hình thang có trung bình cộng hai đáy là 46 m. Nếu mở rộng đáy lớn thêm 12 m và giữ nguyên đáy bé thì thì được thửa ruộng mới có diện tích lớn hơn diện tích thửa ruộng ban đầu là 114 m². Tính diện tích thửa ruộng ban đầu?

Lời giải

Tổng hai đáy là: 46 x 2 = 92m

Goi chiều cao thửa ruộng là h

Diện tích thửa ruộng ban đầu là: 92 x h : 2 = 46 x h

Tổng đáy lớn và đáy bé sau khi mở rộng đáy lớn thêm 12m là: 92 + 12 = 104m

Diện tích thửa ruộng sau khi mở rộng đáy lớn là: 104 x h : 2 = 52 x h

Thửa ruộng mới có diện tích mới lớn hơn 114m²

Suy ra 52 x h – 46 x h = 114 hay h = 19m

Diện tích thửa ruộng ban đầu là: 46 x 19 = 874m²

Một số bài tập để bé tự luyện

Bài 1: Cho hình thang có hai cạnh đáy lần lượt là 6cm và 4cm. Chiều dài của cạnh bên bằng một nửa tổng độ dài hai cạnh đáy. Tính chu vi của hình thang đó, biết rằng hình thang có hai cạnh bên bằng nhau?

Bài 2: Một hình thang có độ dài đáy lớn bằng 4,5dm; độ dài đáy nhỏ bẳng 60cm và chiều cao bằng 8dm. Tính diện tích của hình thang đó.

Bài 3: Có một mảnh đất hình thang với đáy bé là 24m, đáy lớn là 30m. Mở rộng hai dáy về phía bên phải của mảnh đất với đáy lớn thêm 7m, đáy nhỏ thêm 5m thu được mảnh đất hình thang mới với diện tích lớn hơn diện tích ban đầu là 36m2. Tính diện tích mảnh đất hình thang ban đầu.

Bài 4: Tính diện tích hình thang có đáy lớn bằng 50 dm và bằng 80% chiều cao, đáy bé kém đáy lớn 12 dm.

Bài 5: Tính diện tích hình thang có chiều cao bằng 4 dm, đáy bé bằng 80% chiều cao và kém đáy lớn 1,2 dm.

Bài 6: Hình thang có tổng độ dài hai đáy bằng 24 cm, đáy lớn hơn đáy bé 1,2 cm, chiều cao kém đáy bé 2,4 cm. Tính diện tích hình thang.

Bài 7: Hình thang có đáy lớn hơn đáy bé 20,4 dm và bằng 5/3 đáy bé, chiều cao hơn đáy bé 2,1 dm. Tính diện tích hình thang.

BÀI 8: Hình thang có tổng độ dài hai đáy bằng 14,5 dm, đáy lớn gấp rưỡi đáy bé, chiều cao kém đáy bé 2,8 dm. Tính diện tích hình thang.

Bài 9: Hình thang có tổng độ dài hai đáy bằng 30,5 dm, đáy lớn bằng 1,5 lần đáy bé, chiều cao hơn đáy bé 6,2 dm. Tính diện tích hình thang.

Bài 10: Hình thang có tổng độ dài hai đáy bằng 60 m, 1/3 đáy lớn bằng 1/2 đáy bé, chiều cao bằng 80% đáy bé. Tính diện tích hình thang.

Bài 11: Tính diện tích hình thang biết:

a) Độ dài hai đáy lần lượt là 12cm và 8cm; chiều cao là 5cm.

b) Độ dài hai đáy lần lượt là 9,4m và 6,6m; chiều cao là 10,5m.

Bài 12: Một hình thang có đáy nhỏ dài 7cm, đáy lớn dài 17cm được chia thành hai hình thang có đáy chung dài 13cm. Hãy so sánh diện tích hai hình thang có đáy chung nói trên.

Kinh nghiệm tính diện tích hình thang lớp 5 hiệu quả

Để nâng cao hiệu quả trong việc học, giải toán lớp 5 nói chung, chuyên đề tính diện tích hình thang nói riêng thì dưới đây là một số bí quyết để các em có thể tham khảo.

Trang bị nền tảng kiến thức toán học từ nhỏ với Monkey Math

Toán hình không như toán đại số, thường khô khan và nhàm chán. Vậy nên, ngoài việc học kiến thức trên lớp thì ba mẹ có thể trang bị nền tảng kiến thức toán học, cũng như tham khảo phương pháp học tích cực cho bé thông qua ứng dụng Monkey Math.

Được biết, Monkey Math là ứng dụng học toán tư duy tiếng Anh được Monkey phát triển dành cho các bé trong độ tuổi mầm non đến tiểu học. Đặc biệt, ứng dụng sẽ xây dựng nội dung bám sát chương trình GDPT mới nhất của Bộ đưa ra, để đảm bảo hỗ trợ tạo nền tảng toán học vững chắc vừa giúp học toán trên lớp hiệu quả, vừa ứng dụng trong thực tiễn, giải quyết vấn đề dễ dàng hơn.

Điểm đặc biệt của Monkey Math khi học chính là phương pháp dạy. Ứng dụng sẽ áp dụng những phương pháp học tập tích cực để kích thích sự sáng tạo, con tích cực đặt câu hỏi để hiểu tận gốc vấn đề được đưa ra trong Toán học, phương pháp học thông qua trò chơi và sách bài tập bổ trợ sẽ giúp bé ôn luyện kiến thức, tăng sự hứng thú và ghi nhớ tốt hơn trong suốt quá trình học tập.

Ngoài ra, chương trình học cùng Monkey Math sẽ bám sát nhiều chủ đề toán học khác nhau, trong đó sẽ bao gồm đầy đủ những kiến thức về toán hình chi tiết. Đảm bảo, bé sẽ được ôn luyện mọi chủ đề toán học từ cơ bản đến nâng cao.

Đảm bảo, sau khi học cùng Monkey Math sẽ giúp bé:

• Phát triển 5 năng lực Toán học theo chương trình GDPT mới & hình thành thói quen tư duy logic ngay từ nhỏ

• Phát triển tư duy & trí thông minh trong giai đoạn vàng của sự phát triển não bộ

• Xây dựng nền tảng Toán học & hỗ trợ việc học trên lớp hiệu quả

• Phát triển đồng bộ tư duy & ngôn ngữ giúp con học giỏi cả toán và tiếng Anh

Ghi nhớ công thức tính diện tích hình thang lớp 5 qua thơ

Trẻ em thường sẽ ghi nhớ những bài thơ, bài hát có nhịp điệu tốt hơn là học thuộc thông thường. Vậy nên, dưới đây là gợi ý về bài thơ tính diện tích hình thang khá dễ nhớ để các em có thể tham khảo:

"Muốn tính diện tích hình thang

Đáy lớn đáy nhỏ ta đem cộng vào

Cộng vào nhân với chiều cao

Chia đôi lấy nửa thế nào cũng ra"

Luyện tập, thực hành thường xuyên

Học đi đôi với hành luôn là bí quyết thành công trong học tập hay làm việc. Vậy nên, để giúp bé có thể hiểu rõ hơn về kiến thức tính diện tích hình thang toán lớp 5, ba mẹ nên cùng bé luyện tập và thực hành nhiều hơn. Đặc biệt, bạn nên thường xuyên trao đổi với bé những bài toán con chưa hiểu, hay cùng bé tổ chức các cuộc thi giải toán với những phần quà khích lệ,…

Kết luận

Trên đây là những thông tin về công thức tính diện tích hình thang lớp 5 để các em có thể tham khảo. Đây là bài tập khá thông dụng, thường xuất hiện ở các đề thi cũng như ứng dụng trong thực tiễn. Vậy nên, ba mẹ có thể tham khảo để hướng dẫn con học tập hiệu quả hơn nhé.