.png)
Bạn đang loay hoay ôn thi THPT Quốc Gia môn Toán, đặc biệt là phần kiến thức về chuyên đề hàm số mũ và logarit? Đừng lo lắng! Bài viết này sẽ là cẩm nang đầy đủ và chi tiết, giúp bạn chinh phục chuyên đề hóc búa này một cách hiệu quả nhất, từ đó tự tin bước vào kỳ thi và đạt điểm cao.
- Khởi đầu tốt nhất cho con bắt đầu học tiếng Anh. Con học càng sớm càng có lợi thế.
- Tích lũy 1000+ từ vựng mỗi năm và 6000 mẫu câu tiếng Anh trước 10 tuổi.
- Linh hoạt sử dụng trên nhiều thiết bị.
- Thành thạo các kỹ năng tiếng Anh ngay trước 10 tuổi với hơn 1000 đầu truyện, hơn 100 bài học, 300+ sách nói. Nội dung thêm mới mỗi tuần.
- Hơn 1.000 đầu truyện, hơn 300 bài học, gần 300 sách nói - thêm mới mỗi tuần.
- Phát âm chuẩn ngay từ đầu nhờ Monkey Phonics - giúp đánh vần tiếng Anh dễ như tiếng Việt.
- Đánh vần chuẩn nhờ học phần Học Vần - cập nhật theo chương trình mới nhất của Bộ GD&ĐT.
- Đọc - hiểu, chính tả tiếng Việt dễ dàng và nhẹ nhàng hơn ngay tại nhà.
- Bồi dưỡng trí tuệ cảm xúc (EQ) nhờ hơn 450 câu chuyện thuộc 11 chủ đề, nhiều thể loại truyện.
Chuyên đề hàm số mũ và logarit trong cấu trúc đề thi Toán THPT Quốc Gia 2024
Theo thông tin mới nhất, tổng hợp từ đề thi tham khảo THPT Quốc Gia 2024 môn Toán do Bộ GD&ĐT công bố, cấu trúc đề thi Toán THPT Quốc Gia 2024 có độ khó tương đương với kỳ thi năm 2023. Trong đó, nội dung của chuyên đề hàm số mũ và logarit, lũy thừa chiếm khoảng 8 câu trên tổng số 50 câu hỏi có trong đề thi, với 5 câu ở mức độ cơ bản và 3 câu thuộc mức độ thông hiểu đến vận dụng. Chính vì vậy, nếu muốn đạt điểm cao, các thí sinh cần phải nắm chắc phần kiến thức chuyên đề hàm số mũ hàm số logarit từ lý thuyết đến bài tập.
Hàm số lũy thừa
1. Định nghĩa lũy thừa là gì?
2. Một số tính chất của lũy thừa:
Với a, b ≠ 0 và m, n ∈ Z, ta có:
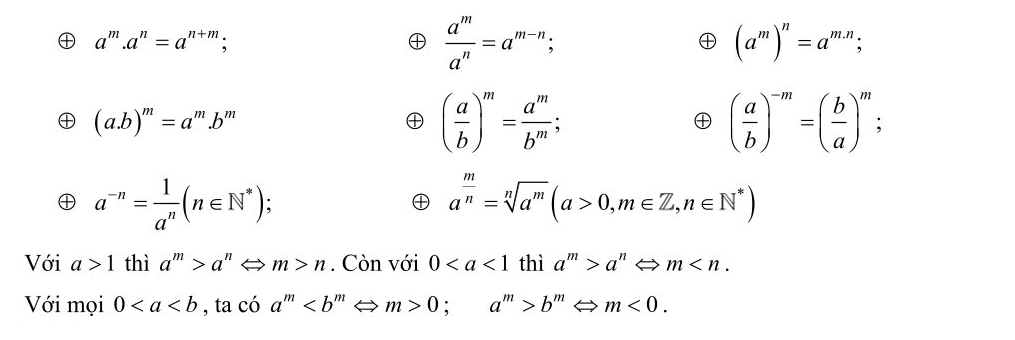
3. Tìm hiểu về căn bậc n trong lũy thừa:
Định nghĩa: Cho số thực b và số nguyên dương n (n ≥ 2). Số a được gọi căn bậc n của số b nếu an = b.
Một số chú ý quan trọng:
Hàm số logarit
1. Định nghĩa logarit là gì?
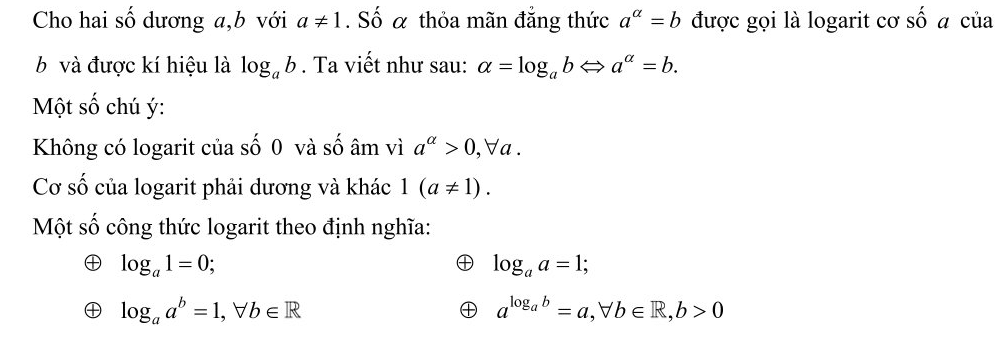
2. Các tính chất của logarit:
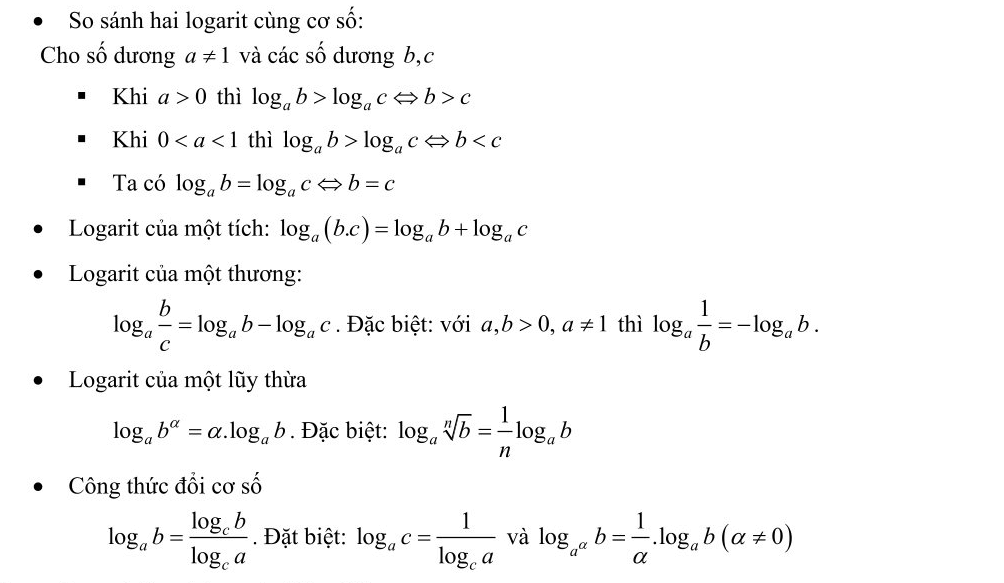
3. Logarit tự nhiên và logarit thập phân:
-
Logarit tự nhiên (hay còn được gọi là logarit Nepe) là logarit cơ số e, được viết là: logeb = lnb.
-
Logarit thập phân là logarit cơ số 10 , được viết là: log10b = logb = lgb.
Hàm số mũ và hàm số logarit
Dưới đây là phần tóm tắt lý thuyết hàm số mũ hàm số logarit mà các thí sinh nên “bỏ túi”:
1. Hàm số mũ:
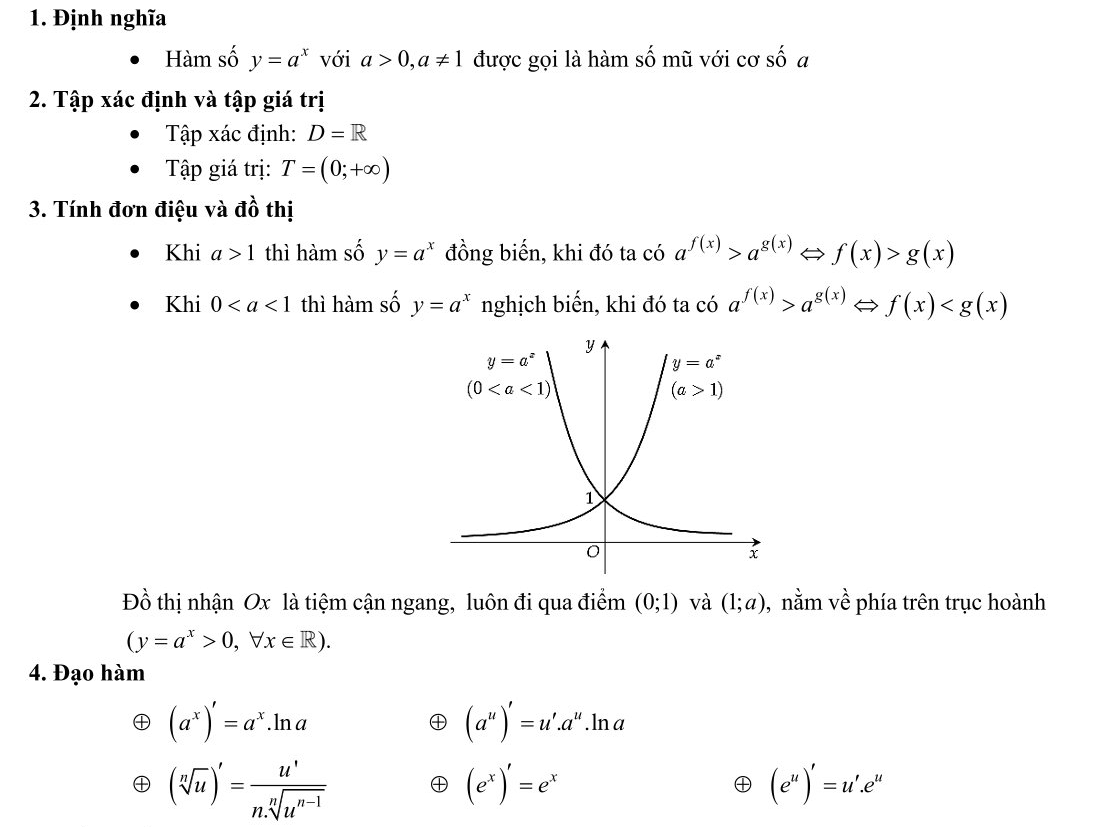
2. Hàm số logarit:
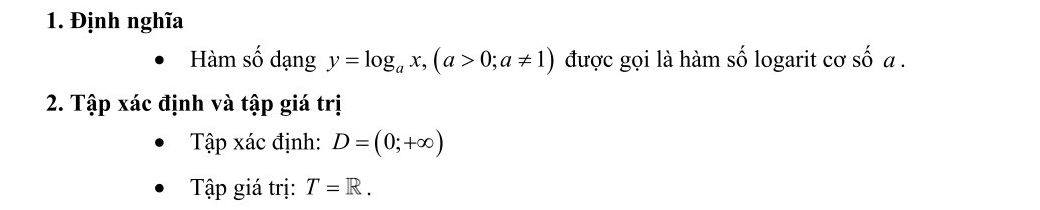
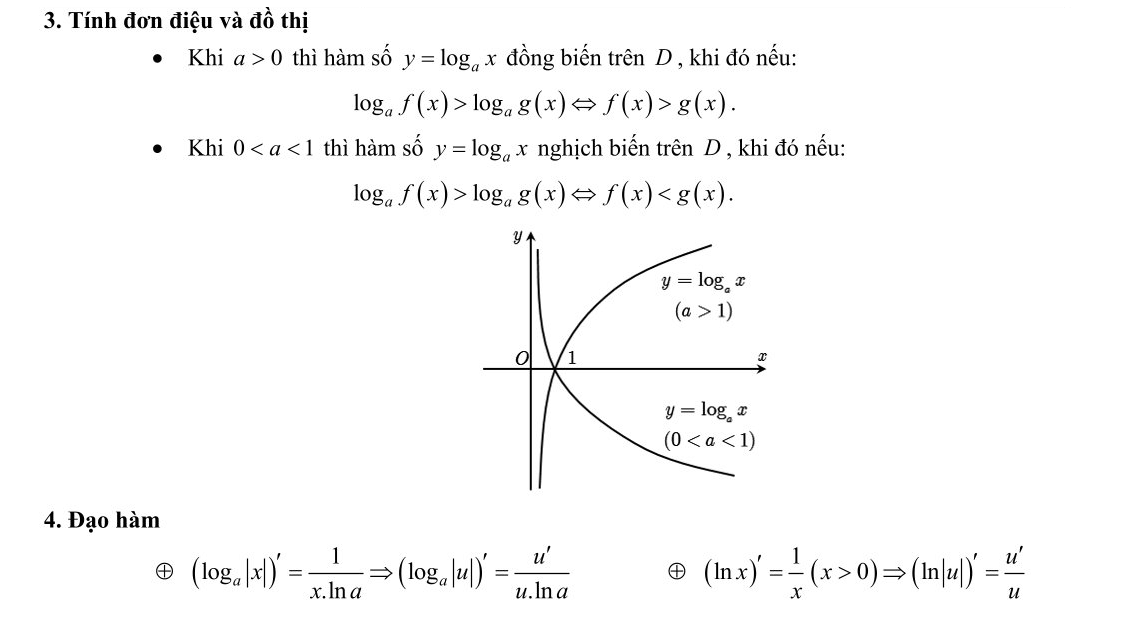
Chuyên đề số phức ôn thi THPT Quốc Gia môn Toán: Lý thuyết & Bài tập
Cấu trúc đề thi Toán THPT Quốc Gia 2024 & Mẹo giải đề hiệu quả
Chuyên đề hàm số ôn thi THPT Quốc Gia môn Toán: Lý thuyết & Dạng bài tập!
Phương trình mũ, phương trình logarit
Ngoài phần ôn tập chương hàm số mũ và logarit kể trên, tiếp theo đây là một số kiến thức về phương trình mũ logarit trong các đề thi Đại Học (thuộc chuyên đề hàm số mũ logarit ôn thi), bao gồm:
Bất phương trình mũ – logarit
Tổng quan lý thuyết về bất phương trình mũ logarit trong đề thi THPT Quốc Gia mà các thí sinh cần ôn tập như:
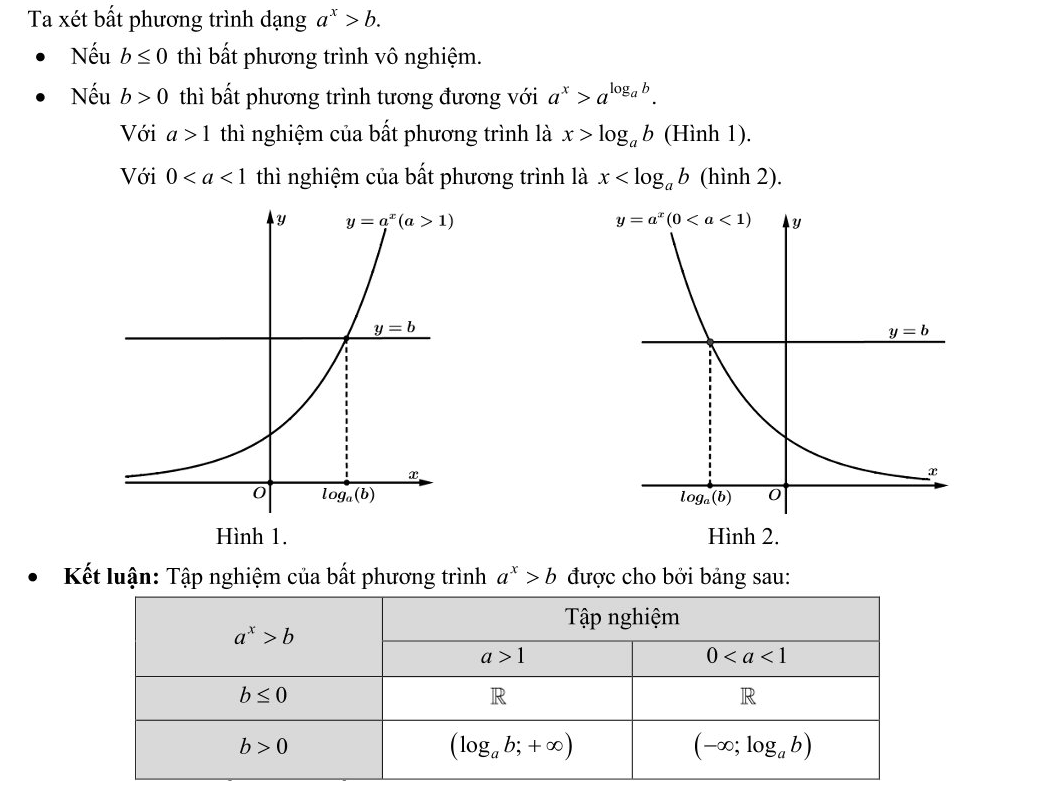
1. Định nghĩa:
Bất phương trình mũ cơ bản có dạng ax > b (hoặc ax ≥ b, ax < b, ax ≤ b ) với a > 0, a ≠ 1.
2. Định lí, quy tắc:
3. Phương pháp đưa về cùng cơ số:
4. Phương pháp đặt ẩn phụ:
5. Phương pháp hàm số, đánh giá:
Xem thêm: Chuyên đề hàm số ôn thi THPT Quốc Gia môn Toán: Lý thuyết & Dạng bài tập!
Dạng bài toán lãi suất trong chuyên đề hàm số mũ và logarit
1. Bài toán theo hình thức lãi kép p, gửi a đồng, lãi suất r một kỳ theo hình thức lãi kép. Tính số tiền thu về sau n kỳ.
-> Công thức tính nhanh: An = a(1 + r)n
2. Bài toán theo hình thức lãi kép, đầu mỗi kỳ gửi a đồng, lãi suất r một kỳ. Tính số tiền thu được sau n kỳ (gồm cả gốc và lãi).
-> Công thức tính nhanh: An = a(1 + r)[((1 + r)n - 1)/r]
3. Bài toán theo hình thức lãi kép, vay A đồng, lãi suất r, trả nợ đều đặn mỗi kỳ số tiền m đồng. Hỏi sau bao nhiêu kỳ thì trả hết số nợ gồm cả gốc và lãi.
-> Công thức tính nhanh: m = [Ar(1 + r)n ]/[(1 + r)n -1]
4. Bài toán theo hình thức lãi kép, gửi a đồng vào tài khoản tiết kiệm, lãi suất r một kỳ. Sau đúng một kỳ rút ra m đồng và các kì sau cũng vậy. Hỏi số tiền còn lại trong tài khoản sau n?
-> Công thức tính nhanh: An = a(1 + r)n - m[((1 + r)n -1)/r]
Lưu ý: Trên đây là một số công thức tổng quát. Trong quá trình giải toán, các thí sinh cần biến đổi linh hoạt các đại lượng mà bài toán yêu cầu dựa trên công thức giải nhanh. Đồng thời kết hợp nhuần nhuyễn các bài toán trong trường hợp đề bài phức tạp.
Với hệ thống kiến thức đầy đủ, phương pháp giải hiệu quả và bài tập vận dụng đa dạng, hy vọng bài viết này đã giúp bạn nắm vững chuyên đề hàm số mũ và logarit - một trong những chuyên đề quan trọng trong kỳ thi THPT Quốc Gia môn Toán. Chúc các bạn học sinh đạt được kết quả cao nhất!
