Công thức tính diện tích hình thoi dễ hiểu và bài tập có lời giải

Diện tích hình thoi là gì? Công thức tính diện tích hình thoi

Theo nguồn từ Wiki thì hình thoi là một hình tứ giác có 4 cạnh bằng nhau. Đây cũng là hình bình hành với hai đường chéo vuông góc với nhau hay hai cạnh kề bằng nhau. 

Còn diện tích hình thoi là phần mặt phẳng của hình mà chúng ta nhìn thấy được, chúng được tính bằng công thức 1 nửa tích của hai đường chéo.

Vậy với một hình thoi ABCD chúng ta sẽ có công thức tính diện tích hình thoi cạnh a là:

S = ½ x (d1 x d2) hoặc S = h x a.

Trong đó:

• S: Là diện tích hình thoi

• d1 và d2:  Lần lượt là đường chéo của hình thoi.

• h: Chiều cao của hình thoi.

• a: Cạnh hình thoi

Ví dụ: Có một cánh diều hình thoi, với hai đường chéo cắt nhau có độ dài lần lượt là 6cm và 8cm. Hỏi diện tích cánh diều hình thoi bao nhiêu?

Áp dụng theo cách tính diện tích hình thoi khi biết cạnh, ta có d1 = 6cm và d2 = 8cm. Suy ra, diện tích cánh diều hình thoi sẽ bằng:

S = ½ x (d1xd2) = 1/2 x (6×8) = 1/2 x 48 = 24 cm2

Một số dạng bài tập tính diện tích hình thoi phổ biến

Dựa vào công thức diện tích hình thoi được xác định bởi nửa tích hai đường chéo. Ta có thể suy ra có nhiều dạng bài tập khác nhau được đưa ra để các em học và chinh phục. Bao gồm:

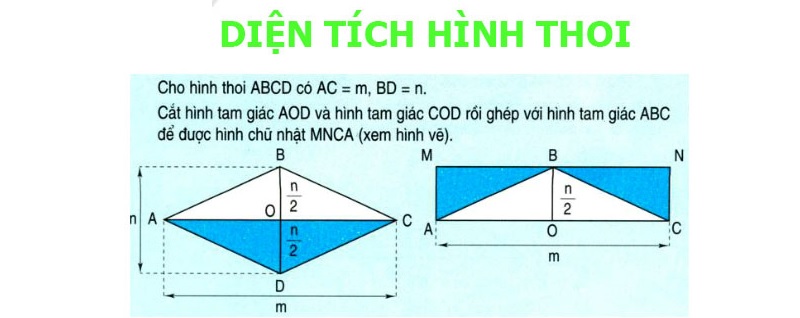
Cách tính diện tích hình thoi dựa vào đường chéo

Công thức tính s hình thoi khi biết đường chéo: S = (đường chéo x đường chéo 2) / 2. Chi tiết về cách tính như sau:

Phương pháp giải: Ta áp dụng đúng công thức tính diện tích hình thoi bằng cách lấy hai đường chéo nhân với nhau rồi chia cho 2.

Muốn tính diện tích hình thoi dựa vào đường chéo, ta thực hiện theo các bước sau đây:

• Bước 1: Xác định độ dài, kích thước của hai đường chéo hình thoi

• Bước 2: Tiến hành nhân độ dài hai đường chéo với nhau.

• Bước 3: Chia tích hai đường chéo cho 2 sẽ được kết quả là diện tích hình thoi.

Cách tính diện tích hình thoi dựa vào chiều cao và cạnh đáy

Diện tích hình thoi tính như nào khi biết chiều cao và cạnh đáy? Cùng tìm hiểu phương pháp giải ngay sau đây:

Phương pháp giải: Hình thoi có đầy đủ tính chất của tứ giác đặc biệt, sở hữu hai cạnh bên và đáy bằng nhau. Vậy nên, với dạng toán cho chiều cao và cạnh đáy, chúng ta có thể áp dụng công thức sau để tính diện tích hình thoi: S = (a + a) x h/2 = a x h 

Trong đó:  

• S: Ký hiệu diện tích hình thoi

• a: Độ dài cạnh bên của hình thoi

• h: Chiều cao của hình thoi

Các bước thực hiện như sau:

• Bước 1:  Xác định độ dài của chiều cao và cạnh đáy của hình thoi. 

• Bước 2: Lấy độ dài chiều cao nhân với độ dài của cạnh đáy. 

Cách tính diện tích hình thoi dựa vào công thức lượng giác 

Phương pháp giải: Muốn tính diện tích hình thoi ta làm thế nào? Nếu xét hình thoi ABCD và gọi độ dài cạnh của hình thoi là a. Lúc này, để xác định được diện tích hình thoi ABCD, chúng ta chỉ cần áp dụng theo diện tích hình thoi công thức sau đây:

S= a². sin α. 

Trong đó:  

S: Ký hiệu diện tích hình thoi

a: Kích thước độ dài cạnh bên

α: Số đo một góc bất kỳ thuộc hình thoi. 

Các bài viết không thể bỏ lỡ

Monkey Math - Ứng dụng học toán tiếng Anh chỉ với 2K/Ngày

Cách tính diện tích hình bình hành đầy đủ chi tiết nhất

Công thức tính diện tích hình chữ nhật và bài tập thực hành chi tiết

Bài tập về tính diện tích hình thoi lớp 5 để bé tự luyện

Dưới đây sẽ là một số bài tập công thức tính diện tích hình thoi lớp 5 để các em cùng nhau luyện tập thêm:

Bài 1:

Hình thoi có hai đường chéo dài 6 cm và 8 cm.
Tính diện tích hình thoi đó.
→ Bài làm: $S = \dfrac{…… × ……}{2} = …… \, (cm^2)$

Bài 2:

Hình thoi có hai đường chéo dài 10 cm và 12 cm.
→ $S = \dfrac{…… × ……}{2} = …… \, (cm^2)$

Bài 3:

Hình thoi có một đường chéo dài 9 cm, đường chéo kia gấp đôi đường chéo thứ nhất.
→ $d_1 = …… \, cm, \, d_2 = …… \, cm$
→ $S = \dfrac{…… × ……}{2} = …… \, (cm^2)$

Bài 4:

Hình thoi có hai đường chéo là 15 cm và 20 cm.
→ $S = \dfrac{…… × ……}{2} = …… \, (cm^2)$

Bài 5:

Một hình thoi có cạnh 10 cm, chiều cao 8 cm.
→ $S = …… × …… = …… \, (cm^2)$

Bài 6:

Hình thoi có diện tích 96 cm², một đường chéo dài 12 cm.
Tính đường chéo còn lại.
→ $96 = \dfrac{12 × ……}{2} \Rightarrow …… = …… \, (cm)$

Bài 7:

Hình thoi có hai đường chéo 5 dm và 9 dm.
→ $S = \dfrac{…… × ……}{2} = …… \, (dm^2)$

Bài 8:

Hình thoi có đường chéo thứ nhất 30 m, đường chéo thứ hai ngắn hơn 10 m.
→ $d_1 = …… \, m, \, d_2 = …… \, m$
→ $S = \dfrac{…… × ……}{2} = …… \, (m^2)$

Bài 9:

Hình thoi có diện tích 200 cm², đường chéo thứ nhất 25 cm.
Tính đường chéo thứ hai.
→ $200 = \dfrac{25 × ……}{2} \Rightarrow …… = …… \, (cm)$

Bài 10:

Một thửa ruộng hình thoi có hai đường chéo là 50 m và 32 m.
→ $S = \dfrac{…… × ……}{2} = …… \, (m^2)$

Đáp án tham khảo:

1. 24 cm²

2. 60 cm²

3. 81 cm²

4. 150 cm²

5. 80 cm²

6. 16 cm

7. 22,5 dm²

8. 300 m²

9. 16 cm

10. 800 m²

Mẹo giúp bé làm bài tập tính diện tích hình thoi hiệu quả

Hình thoi là một trong các loại hình học phổ biến, nên để giúp trẻ có thể học, tiếp thu và thực hành chinh phục được dạng toán tính diện tích này, dưới đây là một số bí quyết hữu ích:

• Giúp bé hiểu công thức: Diện tích hình thoi được tính bằng công thức $S = \frac{d_1 \times d_2}{2}$, trong đó d1​,d2​ là hai đường chéo. Giải thích cho bé hiểu rằng hình thoi có thể chia thành hai tam giác bằng nhau, nên phải chia đôi tích hai đường chéo.

• Minh họa bằng hình thật: Dùng giấy vẽ hình thoi, kẻ hai đường chéo rồi gấp lại để bé thấy rõ hai tam giác bằng nhau, giúp bé hiểu bản chất chứ không học thuộc lòng.

• Hướng dẫn cách làm bài: Nhắc bé đọc kỹ đề, xác định hai đường chéo, viết công thức, thay số vào và ghi đáp số kèm đơn vị (cm², m²…).

• Luyện tập thường xuyên: Cho bé làm nhiều bài tập với các số liệu khác nhau để nhớ công thức lâu hơn và làm nhanh hơn.

• Liên hệ thực tế: Cho bé đo đường chéo của các hình vẽ trên giấy kẻ ô rồi tự tính diện tích, tạo cảm giác học mà chơi.

• Rèn thói quen kiểm tra lại: Sau khi tính xong, khuyến khích bé tự kiểm tra lại phép nhân, phép chia và đơn vị đo.

• Tạo hứng thú học tập: Biến việc luyện tập thành trò chơi, thi tính nhanh diện tích giữa các hình hoặc tô màu hình có đáp án đúng để bé vui học hơn.

Tạo niềm đam mê, hứng thú cho trẻ cùng Monkey Math

Toán học là một bộ môn khá khô khan, với những con số, phép tính, hình học… Chính vì vậy, nếu không tạo cho bé được sự đam mê, hứng thú thì chắc chắn con sẽ rất nhanh chán khi học, cũng như giảm thiểu khả năng tiếp thu.

Vậy nên, ngoài những giờ học toán trên lớp, về nhà bố mẹ có thể cho con cùng học, vui chơi và luyện tập với toán học thông qua Monkey Math. Đây là một trong những ứng dụng dạy toán song ngữ được Monkey phát triển dành cho trẻ mầm non và tiểu học. Với nội dung được bám sát chương trình GDPT mới nhất của Bộ, hướng tới việc phát triển năng lực toàn diện của trẻ thay vì truyền thụ kiến thức. Nên khi theo học cùng Monkey Math, sẽ giúp xây dựng nền tảng và niềm yêu thích toán học của bé tốt hơn.

Đặc biệt, nội dung bài học trên ứng dụng được bám sát vào hơn 60 chủ đề toán, từ số học đến hình học. Tất cả được giảng dạy dưới dạng video, hình ảnh hoạt họa ngộ nghĩnh nên sẽ giúp tăng khả năng tiếp thu của trẻ tốt hơn. Cùng với hơn 10.000 hoạt động tương tác, để giúp bé vừa chơi, vừa học giúp phát triển năng lực quan sát, ghi nhớ, tính toán và tư duy một cách vượt trội.

Chỉ với 2000đ/ngày, nhưng hiệu quả mà Monkey Math mang đến cho sự phát triển trí tuệ, tư duy và ngôn ngữ của bé vượt trội. Nếu bạn cũng đang muốn giúp con yêu của mình đạt được thành quả này, hãy thử cùng con trải nghiệm ứng dụng ngay hôm nay.

FAQ - Một số câu hỏi thường gặp 

Hình thoi là gì?

Hình thoi là tứ giác có bốn cạnh bằng nhau, hai cặp góc đối bằng nhau và hai đường chéo cắt nhau tại trung điểm, vuông góc với nhau.

Đơn vị diện tích của hình thoi là gì?

Tùy theo đơn vị của đường chéo. Nếu đường chéo đo bằng cm nên diện tích là cm², còn nếu đo bằng m thì đơn vị đo diện tích là m²,….

Khi tính diện tích hình thoi, cần chú ý điều gì nhất?

Cần xác định đúng hai đường chéo và đổi về cùng đơn vị đo trước khi tính, ví dụ cùng là cm hoặc m.

Nếu đề bài chỉ cho một đường chéo thì có tính được diện tích không?

Không thể tính được, vì cần biết cả hai đường chéo hoặc có thêm dữ kiện khác mới tính được diện tích.

Học sinh thường sai ở bước nào khi làm bài tính diện tích hình thoi?

Thường sai ở ba chỗ:

• Nhầm số đo hoặc vị trí của đường chéo.
• Quên chia cho 2.
• Quên ghi đơn vị diện tích ở đáp số.

Có mẹo nào giúp bé nhớ nhanh công thức tính diện tích hình thoi không?

Có thể học thuộc bằng câu vè:

“Hai đường chéo nhân nhau chia hai,

Diện tích hình thoi ra ngay tức thì.”

Kết luận

Trên đây là những thông tin về kiến thức cơ bản trong cách tính diện tích hình thoi. Đây là một hình học khá đặc biệt, nhưng việc nắm rõ các công thức liên quan tới hình chính là tiền đề để bé giải bài tập chính xác, cũng như ứng dụng trong thực tế tốt hơn. Nên bố mẹ hãy cùng các bé tham khảo để giải bài tập hình thoi hiệu quả nhé.