Đạo hàm arctan u là một công thức khá khó nhớ và dễ nhầm lẫn, gây khó khăn cho người học. Để có thể nhớ lâu và hiểu bản chất của vấn đề, cùng đi vào tìm hiểu về đạo hàm của arctan u qua bài viết sau đây nhé!
.png)
Video bài giảng được tạo bởi notebooklm.google.com
Đạo hàm arctan u là gì? Lý thuyết & Ví dụ
Đạo hàm arctan u là đạo hàm của hàm hợp. Tất cả các công thức đạo hàm đều liên quan đến hàm hợp u với u là một hàm số với biến số x. Nếu không nhớ rõ và hiểu bản chất của hàm số u, người học sẽ rất dễ nhầm lẫn với đạo hàm của arctan x và từ đó giải sai toàn bài.
Hàm số u(x) với công thức tổng quát là u(x) = ax^n+ bx^m + C.
Tùy thuộc vào phương trình u(x) khác nhau mà công thức đạo hàm arctan u sẽ có một số thay đổi.
Arctan chính là một hàm số ngược trong công thức đạo hàm lượng giác. Để tìm hiểu về đạo hàm arctan u, ta cần tìm hiểu về hàm số y = arctan u.
Tương tự như đạo hàm arctan x thì hàm arctan u chính là hàm y = arctan u. Đây là hàm tiếp tuyến ngược của u với u là một hàm biến số x thuộc tập hợp số thực (x = R). Với hàm tiếp tuyến của y bằng u có công thức là tan y = u thì khi đó thì arctan của u sẽ bằng hàm tiếp tuyến ngược của u với công thức y = arctan u = tan -1 u.
Lấy ví dụ: Cho y = arctan u với u = x = 1. Suy ra y = arctan 1 = tan ^-1 . 1 = π / 4 rad = 45 °.

Ngoài ra, để có thể tìm được arctan u đạo hàm, ta cùng cần phải ràng buộc điều kiện để arctan u có nghĩa. Nó cần đáp ứng một trong các điều kiện mệnh đề sau đây:
-
Mệnh đề 1: Hàm f ( X -> Y ) có hàm ngược khi và chỉ khi F chính là ánh xạ 1-1 từ X đến Y.
-
Mệnh đề 2: Hàm f ( X -> Y ) có hàm ngược ở trên khoảng (a;b) nếu như f là đơn điệu tăng hoặc giảm chắn trên đoạn (a;b).
Xem thêm: Cách tính các dạng đạo hàm arctan thường gặp
Các công thức đạo hàm arctan u (trong chương trình THPT)
Bởi u là một hàm hợp với biến số x, nên khi đạo hàm của arctan u sẽ có thể đạo hàm lần thứ 2, lần thứ 3,... Cùng tìm hiểu về các công thức đạo hàm này nhé!
1. Tìm đạo hàm của hàm arctan u
Công thức đạo hàm arctan u hay còn gọi đạo hàm lần thứ nhất là đạo hàm y’ của hàm số y với y = arctan u. Ta có công thức đạo hàm y’ của arctan u như sau:
![]()
Ví dụ minh họa:
Đề bài: Tính đạo hàm của hàm số y = arctan u với x^2 + 2x + 3
Lời giải: Đạo hàm lần thứ nhất của hàm số y = arctan u là:
![]()
2. Tìm đạo hàm lần thứ 2 của hàm arctan u

Để tìm đạo hàm lần thứ 2 y’’ của hàm số arctan u, ta cần phải tìm lần lượt xong đạo hàm lần thứ nhất rồi sau đó mới tiếp tục đạo hàm kết quả đạt được. Ta có công thức tổng quát như sau:
![]()
Ví dụ về đạo hàm cấp 2:
Tìm đạo hàm cấp 2 của hàm số f (x) = ( 2x - 3 )^5
Lời giải:
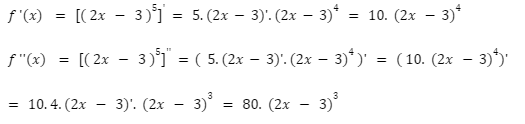
Ví dụ về đạo hàm cấp 2 của arctan u:
Đề bài: Tính đạo hàm cấp 2 của hàm số y = arctan u với x^2 + 2x + 3
Lời giải: Đạo hàm lần thứ 2 của hàm số y = arctan u là:
![]()

Đạo hàm arctan x: Chi tiết công thức & một số dạng bài tập để tự luyện cơ bản

Cách tính các dạng đạo hàm arctan thường gặp: Dễ hiểu, dễ áp dụng nhất

Tổng hợp công thức đạo hàm của các hàm số cơ bản đầy đủ nhất
3. Tìm đạo hàm lần thứ 3 của hàm arctan u
Tương tự, để tìm đạo hàm lần thứ 3 của hàm số y = arctan u, ta cần tìm được đạo hàm lần thứ 2 của hàm số này từ đó đạo hàm tiếp kết quả 1 lần nữa. Ta có công thức như sau:
![]()
Ví dụ về đạo hàm lần thứ 3:
Đề bài: Tìm đạo hàm cấp 3 của hàm số f (x) = ( 2x - 3 )^5
Lời giải:
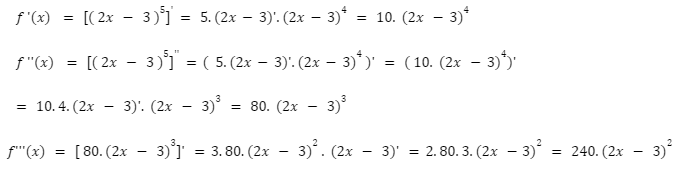
Ví dụ về đạo hàm cấp 3 của arctan u:
Đề bài: Tính đạo hàm cấp 3 của hàm số y = arctan u với x^2 + 2x + 3
Lời giải: Đạo hàm lần thứ 3 của hàm số y = arctan u là:
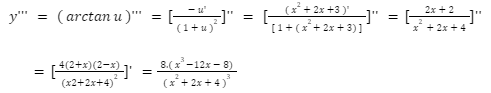
3. Tìm đạo hàm thứ 4 của hàm arctan u
Đạo hàm cấp 4 là đạo hàm của đạo hàm cấp 3 hàm số y = arctan u. Ta có công thức đạo hàm cấp 4 như sau:
![]()
Công thức trên là cách viết công thức thu gọn thể hiện bản chất của đạo hàm cấp 3. Trong lúc tính toán đạo hàm cấp 4, ta cần lần lượt tìm được đạo hàm cấp 1, cấp 2, cấp 3 của hàm số đó.

Ví dụ về đạo hàm lần thứ 4:
Đề bài: Tìm đạo hàm cấp 4 của hàm số f (x) = ( 2x - 3 )^5
Lời giải:
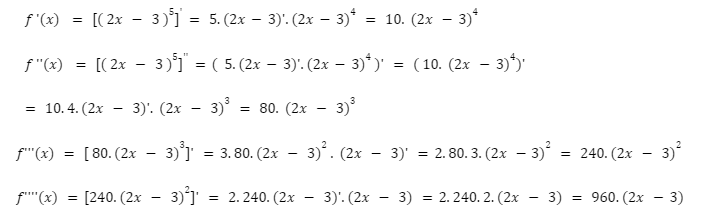
Ví dụ về đạo hàm cấp 4 của arctan u:
Đề bài: Tính đạo hàm cấp 4 của hàm số y = arctan u với x^2 + 2x + 3
Lời giải: Đạo hàm lần thứ 4 của hàm số y = arctan u là:
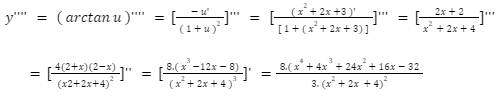
Xem thêm:
- Tổng hợp công thức đạo hàm của các hàm số cơ bản đầy đủ nhất
- Cách tính các dạng đạo hàm arctan thường gặp: Dễ hiểu, dễ áp dụng nhất
Các dạng bài tập đạo hàm arctan u (+ file bài tập)
Để có thể nhuần nhuyễn các bài toán tìm đạo hàm của arctan u, bạn cần phải luyện tập thường xuyên và ghi nhớ các dạng bài tập sau đây:
-
Các mẫu bài tập tìm đạo hàm arctan x.
-
Các mẫu bài tập về tìm đạo hàm cấp 1, cấp 2, cấp 3,... của các hàm số đơn giản.
-
Các mẫu bài tập tìm đạo hàm cấp 1, cấp 2, cấp 3,... của các hàm số phức tạp.
-
Lồng ghép vào công thức chung của đạo hàm arctan u để giải các bài tập.
-
Các chuyên đề bài tập minh họa thực tế.

Bạn đang tìm kiếm một cách học Toán thông minh, sinh động và dễ tiếp cận cho bé? Monkey Math chính là giải pháp hoàn hảo!
Ứng dụng giúp trẻ từ 3-8 tuổi làm chủ Toán học thông qua hơn 10.000+ hoạt động tương tác, 400+ bài học, và hệ thống video hướng dẫn sinh động. Bé không chỉ nắm vững các khái niệm Toán học mà còn phát triển tư duy logic, khả năng giải quyết vấn đề và tiếp cận tiếng Anh toán học một cách tự nhiên.
Hãy để Monkey Math đồng hành cùng bé chinh phục Toán học ngay hôm nay!
Học thêm: Nguyên hàm arctan u
Cho hàm f(x) = arctan(x). Muốn tìm một nguyên hàm F(x) sao cho F'(x)=f(x).
Ta cần tính tích phân bất định ∫ arctan(x) dx. Áp dụng tích phân từng phần để giải.
Bước 1 - Chọn: đặt u = arctan(x) và dv = dx. Khi đó du = dx/(1+x^2) và v = x.
Bước 2 - Công thức:
Theo tích phân từng phần
∫ arctan(x) dx = x·arctan(x) − ∫ x/(1+x^2) dx
Bước 3 - Đổi biến: Đặt t = 1 + x^2 nên dt = 2x dx. Do đó ∫ x/(1+x^2) dx = 1/2 · ln(1+x^2).
Kết luận: F(x) = x·arctan(x) − 1/2 · ln(1+x^2) + C
Ghi chú: vì 1+x^2>0 với mọi x, nên ln|1+x^2| = ln(1+x^2).
[FAQ] - Mọi người cũng hỏi về đạo hàm arctan u
1. Khi nào đạo hàm của arctan u bị vô nghiệm?
Không có điểm vô nghiệm vì mẫu (1 + u²) > 0 với mọi u thực.
2. Có thể áp dụng quy tắc chuỗi khi đạo hàm arctan u không?
Có. Luôn áp dụng quy tắc chuỗi: (arctan u)' = u' / (1 + u²).
3. Arctan u có tính khả vi trên toàn R không?
Có. Hàm arctan u khả vi trên toàn trục số thực.
Trên đây là các công thức chi tiết của đạo hàm arctan u và một số bài tập giúp bạn tự luyện và ghi nhớ công thức đạo hàm của hàm hợp này. Hy vọng bài viết này sẽ giúp bạn hiểu rõ về công thức đạo hàm này!
1. SGK Toán lớp 12 - Chương: Đạo hàm của các hàm số lượng giác ngược (Tham khảo ngày 24/12/2025)
2. SGK Toán lớp 12 - Chương: Đạo hàm (Tham khảo ngày 24/12/2025)
3. Derivative of arctan(u) (Tham khảo ngày 24/12/2025):
https://math.stackexchange.com/questions/1636978/derivative-of-arctanu






![Công thức tính đạo hàm arctan u đơn giản, dễ hiểu [+bài tập]](https://vnmedia2.monkeyuni.net/upload/web/storage_web/24-10-2025_12:17:25_dao-ham-arctan-u.png)
.png)
.png)






.png)