Hàm số bậc 2 là gì? Các dạng bài toán thường gặp trong chương trình học mới nhất

Ôn tập các kiến thức về hàm số

Trước khi đến với kiến thức của hàm số bậc 2, Monkey mời các bạn ôn tập lại các lý thuyết về hàm số lượng giác nói chung ngay dưới đây.

Khái niệm hàm số

Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x, sao cho mỗi giá trị của x ta luôn xác định một giá trị tương đương y, thì y gọi là hàm số của x, và x được gọi là biến số của y.

Kí hiệu của hàm số

Hàm số thường được ký hiệu bằng các chữ cái như f, g và h. Có dạng như sau: y = f (x) với cách đọc là “y bằng f của x”, trong đó: x là đối số của hàm y = f (x), và y là giá trị của hàm y = f (x).

Định nghĩa của hàm số

Cho X, Y là hai tập hợp số, ví dụ là tập hợp số thực, hàm số f xác định trên X, nhận giá trị trong Y là một quy tắc cho tương ứng mỗi số x thuộc X với một số y duy nhất thuộc Y.

Một số tính chất của hàm số

1. Khi x thay đổi mà  y luôn nhận một giá trị thì y gọi là hàm hằng.

2. Hàm số có thể biểu diễn bằng bảng, bằng công thức toán học.

3. Khi y là hàm số của x thì ta có 3 cách viết sau:

• f : X → Y

• f : x → (x)

• y = f(x)

Trong đó:

• • Tập X gọi là miền xác định.

  • Tập Y gọi là miền giá trị.

  • x gọi  là đối số.

  • y là một hàm số.

  • f(x) được gọi là giá trị của hàm f tại x.

Các dạng hàm số

• Hàm số đơn ánh: Một hàm số là đơn ánh khi nó áp dụng lên 2 đối số khác nhau luôn cho 2 giá trị khác nhau. Có nghĩa là với 2 biến x1 và x2 (x1 # x2) thì f(x1) # f(x2).

• Hàm số toàn ánh: Hàm số f được gọi là toàn ánh nếu như với mọi số y thuộc Y ta luôn tìm được ít nhất một số x thuộc X sao cho f(x) = y hay y = f(x)

• Hàm số song ánh: Trong toán học, song ánh, hoặc hàm song ánh, là một hàm số f từ tập X vào tập Y thỏa mãn tính chất, đối với mỗi y thuộc Y, có duy nhất một x thuộc X sao cho f(x) = y.

Hàm số bậc 2 là gì?

Hàm số bậc hai là hàm số có dạng ax^2 + bx + c trong đó a,b,c là các hằng số và (a # 0). Có tập xác định D = R và biệt thức = b2 - 4ac. Hệ số hoàn toàn có thể ở y. Đồng thời, x và y lần lượt là các biến.

Trường hợp có 2 biến x và y, hàm số có dạng: f(x,y) = ax^2 + by^2 + cxy + dx + ey + f

Một số thuật ngữ cần nhớ:

• Hệ số: Hệ số là một nhân tử của một biểu thức trong toán học, một giá trị mà nó xuất hiện phía trước hoặc xuất hiện trong phép nhân với một giá trị khác và thường là một số nhưng không phải biến số.

• Bậc của hàm: Thuật ngữ "đa thức bậc hai" đôi khi có nghĩa là "có bậc là 2", hoặc đôi khi là "có bậc cao nhất là 2". Nếu bậc nhỏ hơn 2, điều này có thể được gọi là "trường hợp suy biến". Thông thường, nghĩa của thuật ngữ sẽ được xác định bởi ngữ cảnh.

• Biến: Biến số là một số có giá trị bất kỳ, và có thể thay đổi giá trị trong một tình huống bất kỳ. Một đa thức bậc hai có có 1 biến duy nhất x (trường hợp đơn biến), hoặc nhiều như biến x, y, và z (trường hợp đa biến). Trên thực tế, người ta thường quy một hàm nhiều biến về các hàm 2 biến để dễ xét.

ĐỪNG BỎ LỠ!! Chương trình học Toán bằng tiếng Anh, giúp phát triển tư duy một cách toàn diện nhất. Nhận ưu đãi lên đến 40% NGAY TẠI ĐÂY!

Cách vẽ các dạng đồ thị hàm số bậc 2

Đồ thị của hàm số bậc 2 có dạng như thế nào? Là câu hỏi phổ biến trong các đề thi lớp 9 và lớp 10. Sau đây là cách vẽ các dạng đồ thị hàm số bậc hai mà bạn cần nắm kỹ.

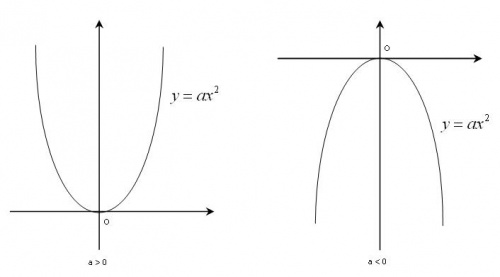
Hàm số bậc hai có dạng y = ax^2

Các bước vẽ đồ thị:

• Bước 1: Xác định tọa độ của đỉnh (0;0)

• Bước 2: Xác định khoảng 5 điểm thuộc đồ thị để vẽ đồ thị chính xác hơn.

• Bước 3: Vẽ parabol

Lưu ý: Khi vẽ parabol cần chú ý đến dấu của hệ số a (a > 0 bề lõm quay lên trên, a < 0 bề lõm quay xuống dưới)

Hàm số bậc hai có dạng y = ax^2+bx+c

Khảo sát hàm số bậc 2

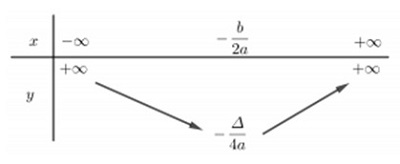
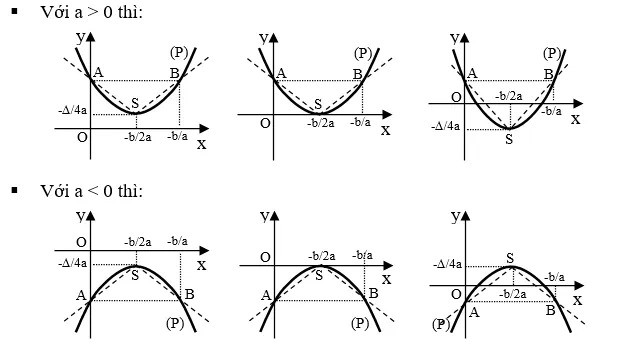
Bảng biến thiên của hàm số y=ax^2+bx+c chia làm 2 trường hợp:

• Trường hợp a > 0, hàm số nghịch biến trên khoảng (−∞ ; −b/2a) và đồng biến trên khoảng (−b/2a ; +∞).

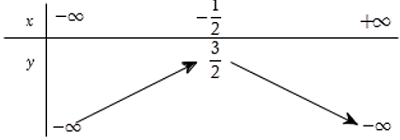
• Trong trường hợp a < 0, hàm số đồng biến trên khoảng (−∞ ;  −b/2a) và nghịch biến trên khoảng (−b/2a ; +∞).

Cách vẽ đồ thị hàm số bậc hai y = ax^2 + bx + c

• Bước 1: Xác định toạ độ đỉnh $I = (-\frac{b}{2a};-\frac{∆}{4a})$
• Bước 2: Xác định trục đối xứng x = (-b)/(2a) và hướng bề lõm của parabol.
• Bước 3: Xác định một số điểm cụ thể của parabol (chẳng hạn, giao điểm của parabol với các trục toạ độ và các điểm đối xứng với chúng qua trục trục đối xứng).
• Bước 4: Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để vẽ parabol.

Các bài viết không thể bỏ lỡ

Monkey Math - Học Toán theo Chương trình GDPT mới cho trẻ Mầm non & Tiểu học

Tổng hợp tất cả các kiến thức về hàm số bậc nhất và dạng bài tập thường gặp

Chi tiết lý thuyết và bài tập ứng dụng hàm số lượng giác, phương trình hàm số lượng giác trong toán học

Khảo sát sự biến thiên của hàm số bậc 2

Hàm số bậc 2 đồng biến khi nào?

• Hàm số f(x) được gọi là đồng biến trên K (K là một khoảng, một đoạn hay nửa đoạn), nếu với mỗi cặp x1, x2 thuộc K mà x1 < x2 thì f(x1) < f(x2).

• Cho hàm số y = f(x) có đạo hàm f’(x) trên K. Nếu f’(x) >= 0, với mọi x thuộc K, f’(x) = 0 chỉ tại một số hữu hạn điểm thì f(x) đồng biến.

Hàm số bậc 2 nghịch biến khi nào?

• Hàm số f(x) được gọi là nghịch biến trên K (K là một khoảng, một đoạn hay nửa đoạn), nếu với mỗi cặp x1, x2 thuộc K mà x1 < x2 thì f(x1) > f(x2).

• Cho hàm số y = f(x) có đạo hàm f’(x) trên K. Nếu f’(x) =< 0, với mọi x thuộc K, f’(x) = 0 chỉ tại một số hữu hạn điểm thì f(x) nghịch biến.

Cực trị của hàm số bậc hai là gì?

Lý thuyết về cực trị của hàm số bậc hai:

Cách lập bảng biến thiên của hàm số bậc hai

• Bước 1: Tìm tập xác định.

• Bước 2: Tính y′. Tìm các điểm tại đó y′ bằng 0 hoặc không xác định.

• Bước 3: Lập bảng biến thiên. Từ bảng biến thiên rút ra kết luận.

Xem thêm: Hàm số tuần hoàn là gì? Cách tính chu kỳ của hàm số lượng giác cực chuẩn

Một số dạng bài tập hàm số bậc 2 thường gặp

Trong chương trình toán học và các đề thi phồ thông, các bạn học sinh sẽ thường gặp một số dạng bài tập về hàm số bậc 2 dưới đây:

Dạng 1: Xác định hàm số bậc hai dạng y = ax^2 + bx +c

Bước 1: Gọi hàm số bậc hai cần tìm có dạng y = ax^2 + bx + c (a ≠ 0)

Bước 2: Dựa vào giả thiết trong đề bài để thiết lập những mối tương quan và tiến hành giải hệ phương trình với các ẩn a, b, c.

Bước 3: Suy ra hàm số cần tìm.

Dạng 2: Lập bảng biến thiên và vẽ đồ thị hàm số

Sau khi lập bảng biến thiên, thì để vẽ đồ thị hàm số y = ax^2 + bx + c (a ≠ 0) ta có thể thực hiện theo các bước sau:

Bước 1: Tìm tọa độ đỉnh I

Bước 2: Tìm trục đối xứng của đồ thị

Bước 3: Tùy đề bài mà tiếp tục tìm tung độ, hoành độ của đồ thị đã cho

Bước 4: Tiến hành vẽ đồ thị theo các điểm đã xác định

Dạng 3: Tìm giá trị cực đại và giá trị cực tiểu của hàm số

Đây là dạng toán mà bạn cần phải dựa theo đồ thị hoặc bảng biến thiên của hàm số y = ax^2 + bx + c (a ≠ 0)  đã cho mà xác định điểm cực đại (max) và điểm cực tiểu (min) trong khoảng giá trị [a;b], tại x = a, x = b, hoặc x = -b/2a.

Dạng 4: Tìm tọa độ giao điểm

Để giải được bài toán tìm tọa độ giao điểm của hai đồ thị f(x) và g(x), ta cần:

• Giải phương trình hoành độ giao điểm f(x) = g(x) (1)
• Trường hợp (1) có n nghiệm thì hai đồ thị có n điểm chung

Ghi chú: Để tìm tung độ giao điểm, thay nghiệm x vào y = f(x) hoặc y = g(x) để tính y.

Để hiểu rõ hơn về các dạng bài tập hàm số bậc 2 trên đây, mời các bạn đến với phần bài tập có lời giải ngay dưới đây.

Một số bài tập xác định hàm số bậc 2 có lời giải

Dưới đây là một số bài toán xác định hàm số bậc 2 có lời giải chi tiết, được Monkey sàng lọc và tổng hợp. Và đây cũng là các dạng bài toán thường xuất hiện trong các đề thi lớp 9 và lớp 10, cũng như kỳ thi THPT Toàn Quốc hằng năm.

Ngoài ra, để xây dựng nền tảng toán học vững chắc cho trẻ, bạn cũng có thể tham khảo ngay ứng dụng học toán bằng tiếng Anh Monkey Math dành cho trẻ từ mầm non đến hết tiểu học. Không chỉ cung cấp các kiến thức toán học chuẩn thuộc chương trình giáo dục phổ thông mới nhất, mà còn là một nền tảng giúp trẻ phát triển khả năng ngôn ngữ (tiếng Anh). Ngoài ra, các tính năng như: Trò chơi, bài tập bổ trợ, phương thức học tích cực,... giúp trẻ tiếp cận mới kiến thức một cách tự nhiên và hiệu quả nhất.

Để được tư vấn tốt nhất, ba mẹ hãy liên hệ Monkey thông qua tổng đài 1900 63 60 52. Hoặc để lại thông tin ngay TẠI ĐÂY để nhận được nhiều ưu đãi lên đến 40% và hàng ngàn tài liệu học tập Miễn Phí.

Trên đây là tất cả nội dung mà Monkey muốn chia sẻ với bạn đọc. Hy vọng rằng với những kiến thức về hàm số bậc 2 này, sẽ giúp bạn tự tin hơn trong các kỳ thi sắp tới. Hãy theo dõi chuyên mục “Kiến thức cơ bản” để nhận thêm các thông tin hữu ích sắp tới nhé!

ĐỪNG BỎ LỠ!! Chương trình học Toán bằng tiếng Anh, giúp phát triển tư duy một cách toàn diện nhất. Nhận ưu đãi lên đến 40% NGAY TẠI ĐÂY!