Công thức tính chu vi hình thang vuông, bài tập và ứng dụng thực tiễn

Ôn tập lý thuyết hình thang vuông

Trước khi đi sâu vào công thức tính chu vi hình thang vuông, chúng ta hãy cùng ôn tập là một số lý thuyết về hình thang vuông mà học sinh cần phải ghi nhớ.

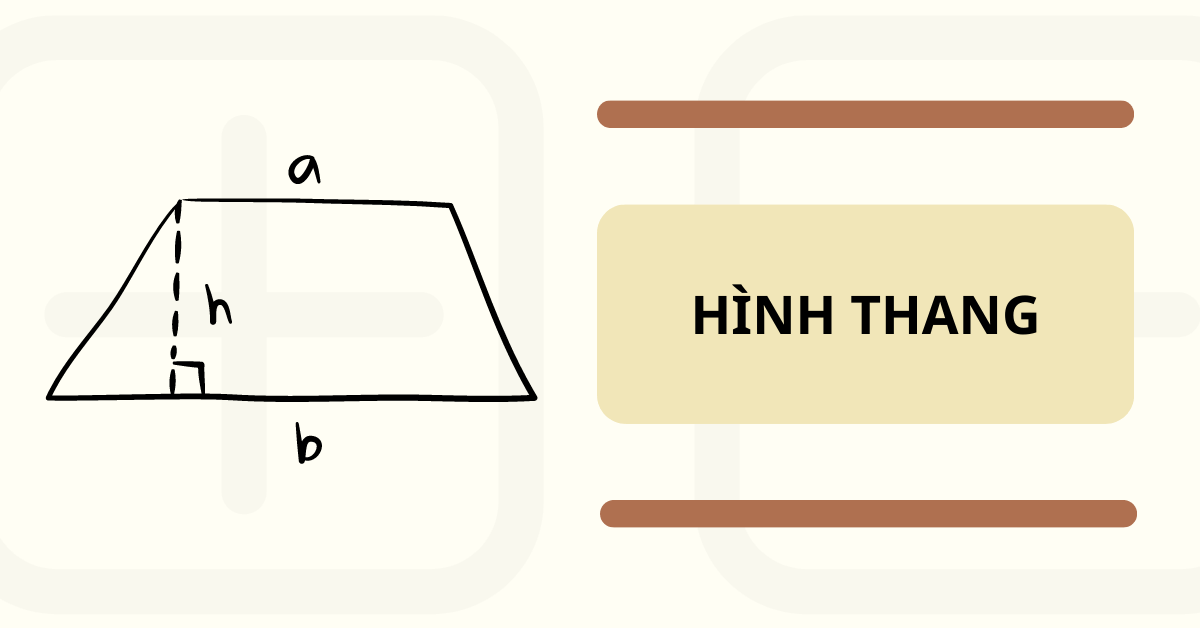
Hình thang vuông là gì?

Hình thang là gì? Hình thang là một tứ giác lồi có hai cạnh đối song song. Trong đó, hai cạnh song song này được gọi là các cạnh đáy của hình thang và hai cạnh còn lại gọi là hai cạnh bên. Dựa vào tính chất của hai cạnh đáy, hình thang có các loại đặc biệt, như: Hình thang cân, hình thang vuông,...

Hình thang vuông là gì? Hình thang vuông là một tứ giác có hai cạnh đối song song (hay hình thang), và có tồn tại một góc vuông. Trong đó, cạnh bên của góc vuông là chính là chiều cao của hình thang. (Như hình minh họa)

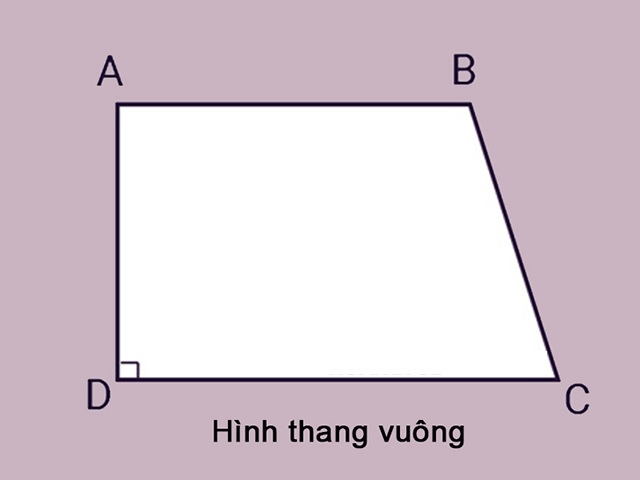
Tính chất của hình thang vuông

Hình thang vuông là một hình thang đặc biệt với những tính chất riêng biệt. Dưới đây là một số tính chất nổi bật của hình thang vuông:

• Trong hình thang vuông, hai cạnh bên không song song, nhưng một trong hai cạnh này vuông góc với hai đáy. Điều này nghĩa là nó tạo ra một góc vuông (hay 90 độ) so với cạnh đáy.

• Đường cao của hình thang vuông chính là cạnh bên tạo góc vuông với hai đáy.

• Nếu kéo dài hai cạnh bên của hình thang vuông, chúng sẽ cắt nhau tại một điểm. Tuy nhiên, cạnh chéo này không chia hình thang thành hai tam giác có diện tích bằng nhau.

• Trong hình thang vuông, có ít nhất một góc vuông. Tuy nhiên, cần chú ý rằng không phải tất cả các góc trong hình thang vuông đều là góc vuông.

Dấu hiệu nhận biết hình thang vuông

Hình thang vuông là một dạng hình thang đặc biệt và dễ nhận biết với các dấu hiệu sau:

• Một góc vuông: Hình thang vuông phải có ít nhất một cạnh bên tạo thành một góc vuông (90 độ) với một cạnh đáy.

• Hai cạnh đáy song song: Giống như mọi hình thang, hình thang vuông cũng có hai cạnh đáy chạy song song với nhau.

Chú ý: Trong hình thang vuông, nếu biết một góc là vuông, các góc còn lại sẽ không cùng bằng 90 độ. Nếu một cạnh bên tạo góc vuông với cả hai đáy, thì hình đó không phải là hình thang vuông mà là hình chữ nhật.

Công thức tính chu vi hình thang vuông

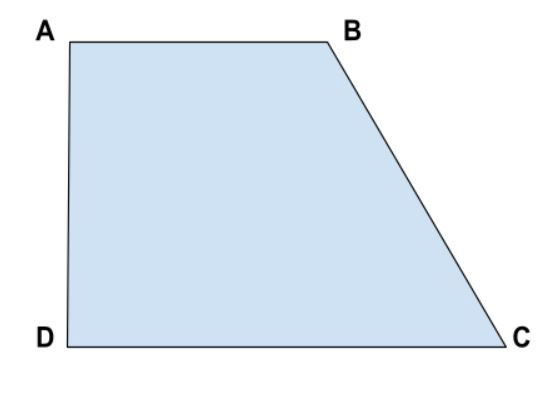
Chu vi hình thang vuông là tổng độ dài của các cạnh của hình thang vuông.

Công thức tính chu vi hình thang vuông:

P = a + b + c + d

Trong đó:

• P là chu vi hình thang vuông.

• a và b là hai cạnh đáy của hình thang vuông.

• c và d là hai cạnh bên của hình thang vuông.

Ví dụ: Hình thang ABCD có AB // CD, AB = 4cm, CD = 8cm, AD = 5cm, BC = 6cm. Tính chu vi hình thang ABCD.

Ta có:

Hai cạnh đáy là AB = 4cm và CD = 8cm.

Hai cạnh bên là AD = 5cm và BC = 6cm.

Chu vi hình thang ABCD là:

P = a + b + c + d = 4 + 8 + 5 + 6 = 23 cm

Như vậy, chu vi hình thang vuông ABCD là 23 cm.

Bên cạnh công thức tính chu vi hình thang vuông, thì bạn cũng cần ghi nhớ một công thức khác cũng không kém phần quan trọng, đó là diện tích hình thang vuông. Cụ thể như sau:

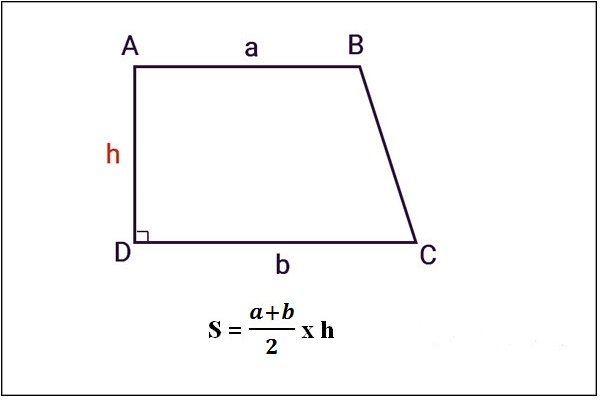
Diện tích hình thang vuông bằng một nửa tích của hai cạnh đáy và chiều cao.

Công thức tính diện tích hình thang vuông:

S = (1/2) * (a + b) * h

Trong đó:

• S là diện tích hình thang vuông.

• a và b là hai cạnh đáy của hình thang vuông.

• h là chiều cao của hình thang vuông.

Ví dụ: Hình thang ABCD có AB // CD, AB = 4cm, CD = 8cm, AD = 5cm. Tính diện tích hình thang ABCD.

Ta có:

Hai cạnh đáy là AB = 4cm và CD = 8cm.

Chiều cao của hình thang là AD = 5cm.

Diện tích hình thang ABCD là:

S = (1/2) * (a + b) * h = (1/2) * (4 + 8) * 5 = 30 cm2

Như vậy, diện tích hình thang vuông ABCD là 30 cm2.

Các bài viết không thể bỏ lỡ

Công thức tính diện tích hình thang vuông & bài tập có lời giải chi tiết

Hình thang vuông: Khái niệm, tính chất, dấu hiệu nhận biết & các công thức tính

Hình thang là gì? Tính chất, dấu hiệu nhận biết hình thang

Các bài tập ví dụ về phép tính chu vi hình thang vuông

Dưới đây là một số bài tập ví dụ về phép tính chu vi hình thang vuông:

Bài 1: Cho hình thang vuông EFGH với EF = 5cm, GH = 10cm, EG = 7cm và FH = 6cm. Tính chu vi hình thang EFGH.

Giải:

Theo công thức tính chu vi hình thang vuông, ta có:

P=5+10+7+6=28cm

Chu vi hình thang vuông EFGH là 28 cm.

Bài 2: Hình thang vuông IJKL có IJ = 9cm, KL = 11cm, IK = 8cm và JL = 7cm. Tính chu vi hình thang IJKL.

Giải:

Theo công thức tính chu vi hình thang vuông, ta có:

P=9+11+8+7=35cm

Chu vi hình thang vuông IJKL là 35 cm.

Bài 3: Hình thang vuông có hai cạnh đáy dài 12cm và 15cm, hai cạnh bên lần lượt là 9cm và 10cm. Tính chu vi hình thang.

Giải:

Theo công thức tính chu vi hình thang vuông, ta có:

P=12+15+9+10=46cm

Chu vi hình thang vuông đó là 46 cm.

Bài 4: Cho hình thang vuông MNOP với MN = 8cm, OP = 9cm, MO = 6cm và NP = 7cm. Tính chu vi hình thang MNOP.

Giải:

Theo công thức tính chu vi hình thang vuông, ta có:

P=8+9+6+7=30cm

Chu vi hình thang vuông MNOP là 30 cm.

Bài 5: Hình thang vuông có hai cạnh đáy là 6cm và 7cm, hai cạnh bên dài 4cm và 5cm. Tính chu vi hình thang.

Giải:

Theo công thức tính chu vi hình thang vuông, ta có:

P=6+7+4+5=22cm

Chu vi hình thang vuông là 22 cm.

Ngoài ra, còn rất nhiều bài tập ví dụ khác về phép tính chu vi hình thang vuông. Để giải các bài tập này, cần nắm vững công thức tính chu vi hình thang vuông và áp dụng linh hoạt vào từng bài toán cụ thể.

Xem thêm:

1. Monkey Math - Ứng dụng học toán bằng tiếng Anh số 1 cho trẻ mầm non & tiểu học
2. Hình thang vuông: Khái niệm, tính chất, dấu hiệu nhận biết & các công thức tính
3. Công thức tính chu vi hình vuông và bài tập vận dụng chi tiết

Ứng dụng thực tiễn của chu vi hình thang vuông

Chu vi hình thang vuông là một trong những kiến thức toán học cơ bản được ứng dụng rộng rãi trong thực tiễn. Một số ứng dụng thực tiễn của chu vi hình thang vuông bao gồm:

• Trong xây dựng: Chu vi hình thang vuông được sử dụng để tính toán lượng vật liệu cần thiết để xây dựng các công trình có hình dạng hình thang vuông, chẳng hạn như cầu thang, mái nhà, hay các công trình dân dụng khác.

Ví dụ: Để xây dựng một cầu thang có hình thang vuông, người ta cần tính toán lượng vật liệu cần thiết để xây dựng các bậc thang, tay vịn và lan can. Để tính toán lượng vật liệu cần thiết, người ta cần biết chu vi của hình thang vuông.

• Trong thiết kế: Chu vi hình thang vuông được sử dụng để tính toán kích thước của các vật dụng, đồ dùng có hình dạng hình thang vuông, chẳng hạn như bàn ghế, giường ngủ, hay các đồ nội thất khác.

Ví dụ: Để thiết kế một chiếc bàn có hình thang vuông, người ta cần tính toán kích thước của mặt bàn, chân bàn, và các thanh ngang. Để tính toán kích thước của các bộ phận này, người ta cần biết chu vi của hình thang vuông.

• Trong đo lường: Chu vi hình thang vuông được sử dụng để đo đạc các khoảng cách, kích thước, hay diện tích của các vật thể có hình dạng hình thang vuông.

Ví dụ: Để đo đạc chiều dài của một mái nhà có hình thang vuông, người ta cần sử dụng thước dây để đo chu vi của mái nhà.

Tóm lại, chu vi hình thang vuông là một kiến thức toán học cơ bản có ứng dụng rộng rãi trong thực tiễn. Việc nắm vững kiến thức này, không chỉ giúp chúng ta giải quyết các bài tập trên trường học mà còn xử lý các bài toán thực tiễn một cách hiệu quả.