Hình thoi lớp 4 và những kiến thức mà học sinh phải thuộc lòng

Định nghĩa hình thoi lớp 4

Hình thoi được hiểu là một hình tứ giác có 4 cạnh bằng nhau (trong đó hai cặp cạnh đối nhau thì song song với nhau), hay hình thoi là một hình bình hành có 2 cạnh liền kề bằng nhau (hoặc có 2 được chéo vuông góc với nhau).

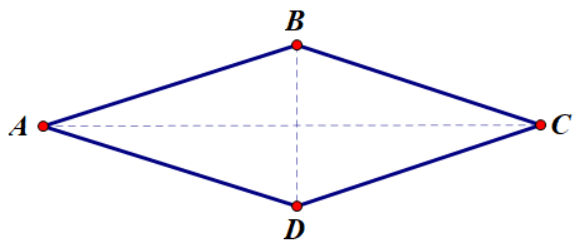
Các tính chất của hình thoi

Dưới đây là một số tính chất cơ bản về hình thoi lớp 4 mà bạn cần nhớ:

• Một hình thoi sẽ có tất cả các tính chất của hình bình hành, như: cạnh đối nhau sẽ song song và bằng nhau, góc đối nhau sẽ bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường.

• Hình thoi có hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường.

• Hai đường chéo của một hình thoi chia các góc của nó thành hai phần bằng nhau.

• Hai đường chéo chia hình thoi thành 4 tam giác bằng nhau.

Dấu hiệu nhận biết hình thoi

Để nhận biết đâu là một hình thoi, bạn có thể dựa vào một số dấu hiệu dễ thấy sau đây:

Hình thoi là một hình tứ giác đặc biệt

• Một tứ giác có 4 cạnh bằng nhau chính là hình thoi.

• Một tứ giác có 2 đường chéo là đường phân giác của tất cả các góc là hình thoi.

• Một tứ giác có 2 đường chéo là đường trung trực (vuông góc và cắt nhau tại trung điểm của mỗi đường) là hình thoi.

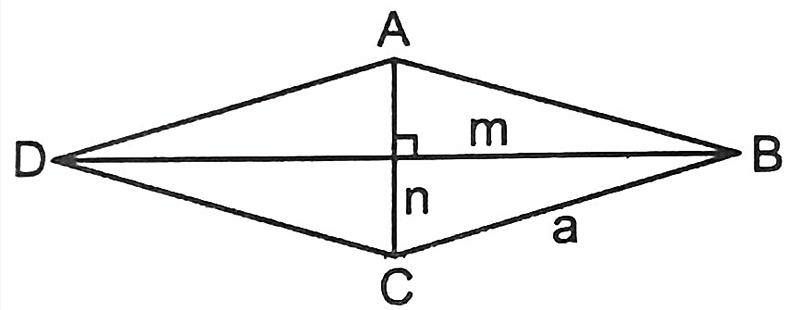
Hình thoi là một hình bình hành đặc biệt

• Một hình bình hành có hai cạnh bên (hai cạnh liền kề) bằng nhau là hình thoi.

• Một hình bình hành có hai đường chéo vuông góc với nhau thì chính là hình thoi.

• Đường chéo của một hình bình hành chia các góc thành hai phần bằng nhau (đường phân giác) thì đó là hình thoi.

Cần nhớ: Vì hình thoi là một dạng đặc biệt của hình bình hành, nên hình thoi sẽ có đầy đủ các tính chất cần có của hình bình hành và có thêm một số tính chất được liệt kê bên trên.

Công thức tính chu vi, diện tích hình thoi lớp 4

Đối với các bài tập toán lớp 4 hình thoi, thì các công thức thường được sử dụng nhất chính là chu vi và diện tích của hình thoi. Dưới đây là chi tiết về công thức và ví dụ.

Công thức tính chu vi hình thoi lớp 4

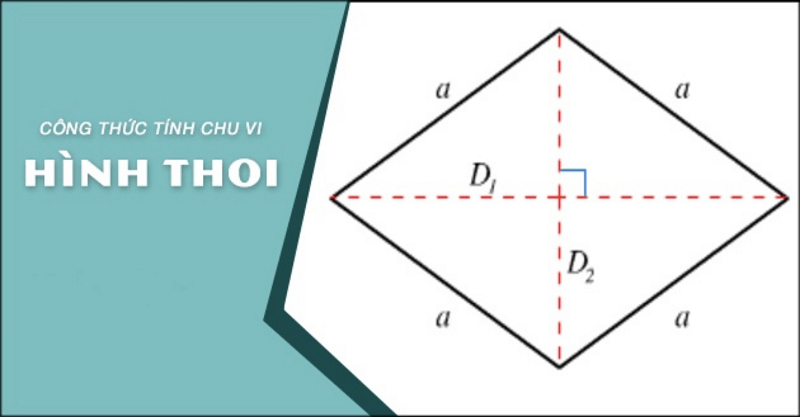
Chu vi của hình thoi chính là độ dài của phần viền bên ngoài hình thoi, được tính bằng cách cộng độ dài của 4 cạnh lại với nhau, hay nói cách khác chu vi hình thoi bằng độ dài của một cạnh nhân với 4. Công thức tính:

P = a.4

Trong đó:

• P: chu vi hình thoi

• a: chiều dài một cạnh bất kỳ

Ví dụ: Giả sử một hình thoi có độ dài cạnh là 5cm. Hãy tính chu vi của hình thoi này.

Theo công thức, chu vi hình thoi (P) bằng độ dài một cạnh (a) nhân với 4.

P = a.4 = 5. 4 = 20cm

Vậy, chu vi của hình thoi có độ dài cạnh là 5cm là 20cm.

Công thức tính diện tích hình thoi lớp 4

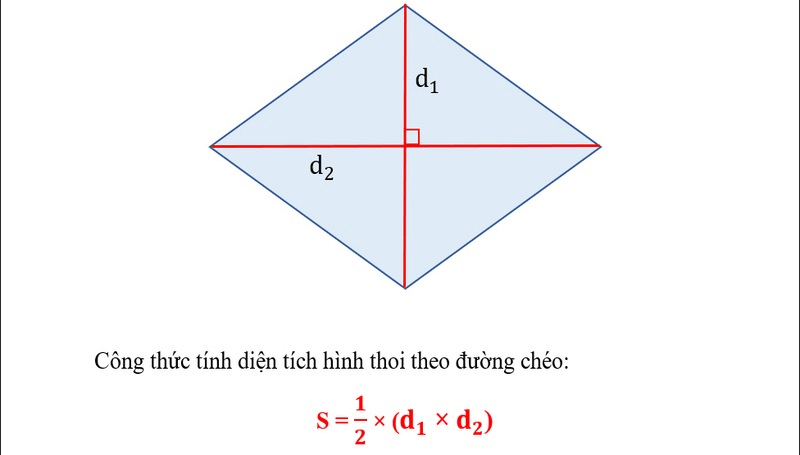
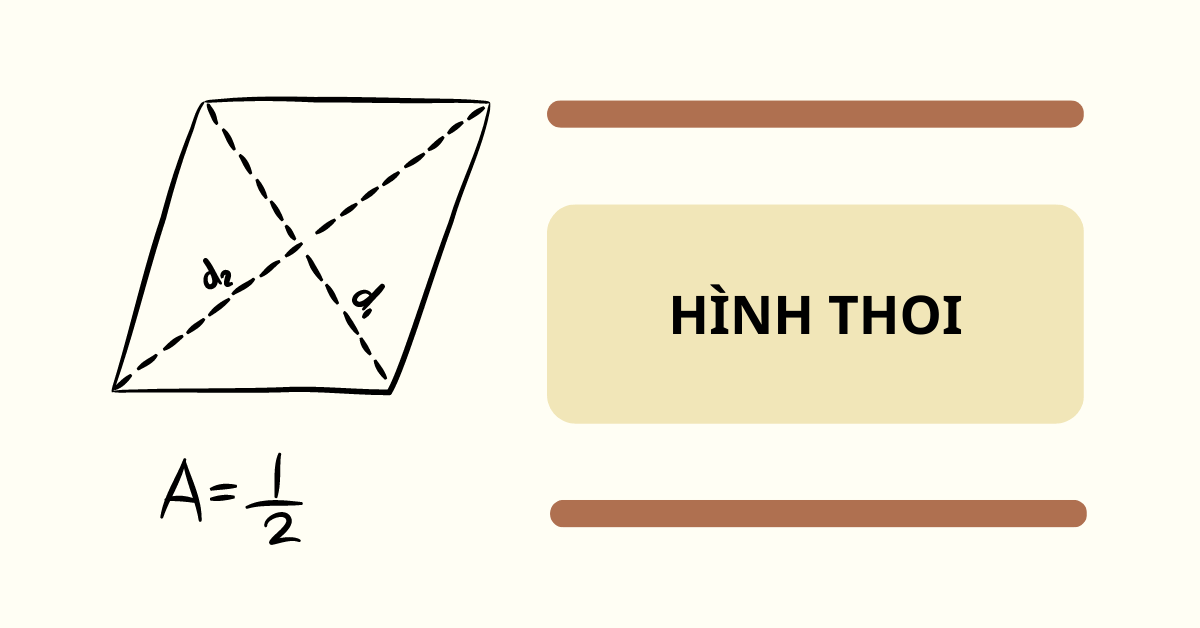
Diện tích hình thoi chính là phần mặt phẳng (bao gồm cả bên trong lẫn phần viền) của hình, được tính bằng cách lấy một nửa tích hai đường chéo của chính nó hoặc bằng chiều cao nhân với cạnh bên. Công thức tính:

S = 1/2(d2.d2) = h.a

Trong đó:

• S: diện tích của hình thoi

• d1, d2: lần lượt là độ dài hai đường chéo của hình thoi

• h: chiều cao của hình thoi (đoạn thẳng vuông góc kẻ từ một đỉnh đến cạnh đáy)

• a: cạnh đáy (là cạnh bất kỳ được chọn và vuông góc với chiều cao)

Ví dụ 1: Giả sử hai đường chéo của một hình thoi có độ dài lần lượt là 8cm và 6cm. Hãy tính diện tích của hình thoi này.

Theo công thức, diện tích hình thoi (S) bằng một nửa tích hai đường chéo.

S = 1/2(d1. d2) = 1/2(8 x 6) = 1/2 x 48 = 24cm2

Vậy, diện tích của hình thoi với hai đường chéo có độ dài là 8cm và 6cm là 24cm².

Ví dụ 2: Giả sử chiều cao của một hình thoi là 10cm và cạnh đáy là 7cm. Hãy tính diện tích của hình thoi đó.

Theo công thức, diện tích hình thoi (S) bằng chiều cao (h) nhân với cạnh đáy (a).

S = h.a = 10 x 7 = 70cm2

Vậy, diện tích của hình thoi có chiều cao là 10cm và cạnh đáy là 7cm là 70cm².

Các bài viết không thể bỏ lỡ

Hình thoi: Khái niệm, dấu hiệu nhận biết và các công thức tính chi tiết nhất

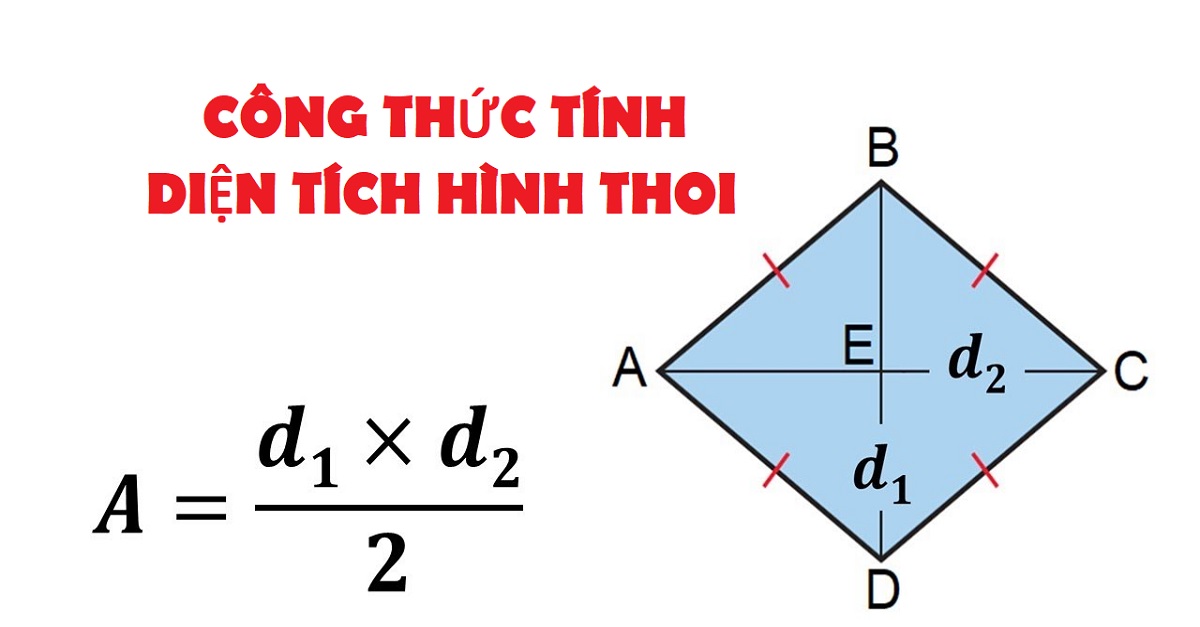
Công thức tính diện tích hình thoi và hướng dẫn giải bài tập chi tiết

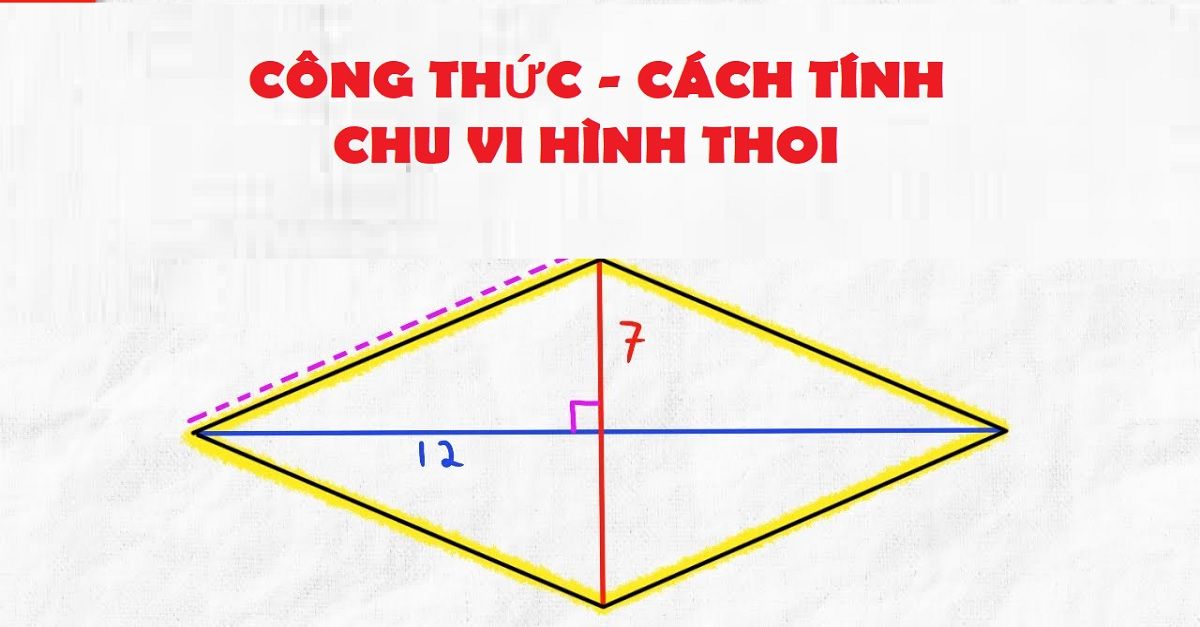
Công thức tính chu vi hình thoi và hướng dẫn giải bài tập chi tiết

Giải bài tập hình thoi lớp 4 trong 140, 141 SGK

Bài 1, trang 140 - 141, hình thoi lớp 4 (SGK)

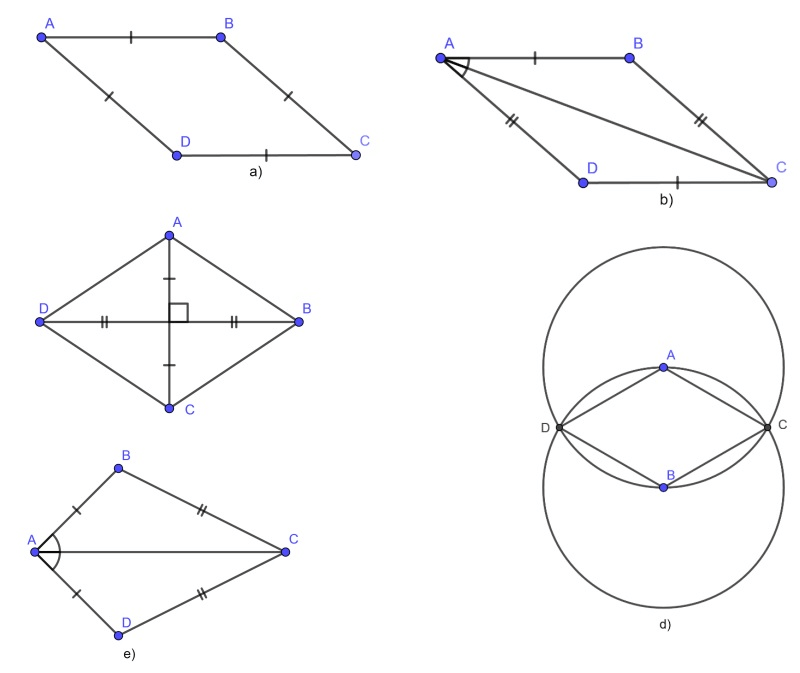
Đề bài: Trong các hình dưới đây

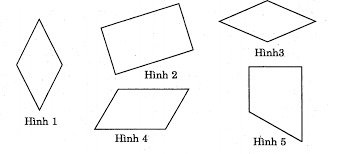
Hình nào là hình thoi? Hình nào là hình chữ nhật?

Đáp án:

(Dựa vào những tính chất đã được học, sau đó nhận dạng và trả lời câu hỏi.)

• Hình 1, Hình 3 là hình thoi.

• Hình 2 là hình chữ nhật.

• Hình 4 là hình bình hành.

• Hình 5 là hình thang vuông.

Bài 2, trang 140 - 141, hình thoi lớp 4 (SGK)

Đề bài: Trong hình thoi ABCD, AC và BD là hai đường chéo của hình thoi chúng cắt nhau tại điểm O.

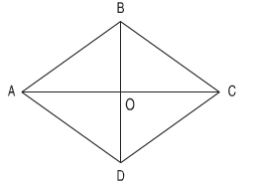
a. Dùng êke để kiểm tra xem hai đường chéo có vuông góc với nhau hay không.

b. Dùng thước có vạch chia xăng-ti-mét để kiểm tra xem hai đường chéo có cắt nhau tại trung điểm của mỗi đường hay không.

Đáp án:

(Dùng êke và thước có vạch chia xăng-ti-mét để kiểm tra theo yêu cầu của đề bài.)

a. Dùng êke kiểm tra ta thấy hai đường chéo vuông góc nhau.

b. Hai đường chéo cắt nhau tại trung điểm của mỗi đường vì khi dùng thước có vạch chia xăng-ti-mét để kiểm tra ta có: OA = OC = 3cm  ;    OB = OD = 2cm.

Nhận xét: Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

Bài 3, trang 140 - 141, hình thoi lớp 4 (SGK)

Đề bài: Thực hành gấp và cắt giấy (theo hình vẽ)  để tạo thành hình thoi.

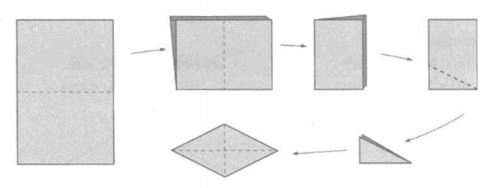
Đáp án:

Tại đây, bạn cần quan sát kỹ các nếp gấp và những bước hướng dẫn của hình, tiếp theo hãy thực hành từng bước một, nếu kết quả khác hình vẽ hãy quan sát và thực hiện lại cho đến khi đúng.

Một số bài tập tính chu vi, diện tích hình thoi thường gặp (có đáp án)

Bài 1: Tính diện tích của hình thoi biết độ dài hai đường chéo lần lượt là 16cm và 20cm.

Bài giải:

Diện tích của hình thoi là:

(16 x 20) : 2 = 160 (cm2)

Đáp số: 160cm2

Bài 2: Một hình thoi có độ dài đường chéo lớn là 12dm, diện tích hình thoi là 48dm2. Tính độ dài đường chéo còn lại của hình thoi.

Bài giải:

Độ dài đường chéo còn lại của hình thoi là:

(48 x 2) : 12 = 8(dm)

Đáp số: 8dm

Bài 3: Hình thoi ABCD có độ dài đường chéo AC = 15cm, độ dài đường chéo BD bằng 2/3 độ dài đường chéo AC. Tính diện tích hình thoi ABCD.

Bài giải:

Độ dài đường chéo BD là:

(15 : 3) x 2 = 10 (cm)

Diện tích hình thoi ABCD là:

(15 x 10) : 2 = 75(cm2)

Đáp số: 75cm2

Xem thêm:

1. Monkey Math - Ứng dụng học toán bằng tiếng Anh số 1 cho trẻ mầm non & tiểu học
2. Chi tiết cách tính diện tích hình bình hành lớp 4 và bài tập có lời giải

Bài 4: Cho hình thoi có diện tích bằng diện tích hình vuông cạnh 10cm, biết 1 đường chéo hình thoi bằng độ dài cạnh hình vuông. Tính độ dài đường chéo còn lại của hình thoi.

Bài giải:

Diện tích của hình vuông hay diện tích của hình thoi là:

10 x 10 = 100(cm2)

Độ dài đường chéo còn lại của hình thoi là:

100 x 2 : 10 = 20(cm)

Đáp số: 20cm

Bài 5: Một hình thoi có tổng độ dài hai đường chéo là 270cm, biết độ dài đường chéo ngắn bằng 4/5 độ dài đường chéo dài. Tính diện tích hình thoi.

Bài giải:

Tổng số phần bằng nhau là:

4 + 5 = 9 (phần)

Độ dài đường chéo dài là:

270 : 9 x 5 = 150(cm)

Độ dài đường chéo ngắn là:

270 – 150 = 120(cm)

Diện tích của hình thoi là:

150 x 120 : 2 = 9000(cm2)

Đáp số: 9000cm2

Monkey khuyến khích bạn nên tự thực hiện các bài tập tính chu vi và diện tích hình thoi trên đây, sau đó mới tra đáp án và cách thức giải. Hy vọng những kiến thức về hình thoi lớp 4 này sẽ giúp ích cho bạn trong quá trình học. Hãy lưu bài viết này lại như một cẩm nang bạn nhé!