Đạo hàm bằng 0 là trường hợp khá đặc biệt trong quá trình tính đạo hàm. Vậy nên, học sinh cũng cần phải nắm rõ đặc điểm, công thức để giúp nhận biết và tính toán chúng chính xác nhất.
- Khởi đầu tốt nhất cho con bắt đầu học tiếng Anh. Con học càng sớm càng có lợi thế.
- Tích lũy 1000+ từ vựng mỗi năm và 6000 mẫu câu tiếng Anh trước 10 tuổi.
- Linh hoạt sử dụng trên nhiều thiết bị.
- Thành thạo các kỹ năng tiếng Anh ngay trước 10 tuổi với hơn 1000 đầu truyện, hơn 100 bài học, 300+ sách nói. Nội dung thêm mới mỗi tuần.
- Hơn 1.000 đầu truyện, hơn 300 bài học, gần 300 sách nói - thêm mới mỗi tuần.
- Phát âm chuẩn ngay từ đầu nhờ Monkey Phonics - giúp đánh vần tiếng Anh dễ như tiếng Việt.
- Đánh vần chuẩn nhờ học phần Học Vần - cập nhật theo chương trình mới nhất của Bộ GD&ĐT.
- Đọc - hiểu, chính tả tiếng Việt dễ dàng và nhẹ nhàng hơn ngay tại nhà.
- Bồi dưỡng trí tuệ cảm xúc (EQ) nhờ hơn 450 câu chuyện thuộc 11 chủ đề, nhiều thể loại truyện.
Khái niệm đạo hàm bằng 0 là gì?
Trong chuyên đề đạo hàm, khi một đạo hàm dương (khi hàm số đang tăng) rồi bỗng nhiên chuyển sang thành đạo hàm âm (hàm số giảm), có nghĩa là nó đã đi qua vị trí mà tại đó có một hàm số đạt được giá trị cực đại, đây cũng chính là vị trí đạo hàm bằng 0.
Ngoài ra, trong giải tích, số 0 được xem là một hằng số, nên khi đạo hàm hằng số thì sẽ bằng 0.
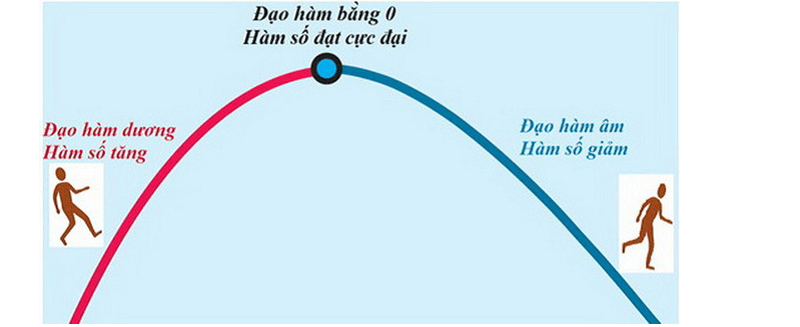
Vì sao đạo hàm của bất cứ hằng số nào cũng đều bằng 0?
Về mặt lý thuyết, đạo hàm của một hàm số y với biến x nào đó trong y chính là việc xem xét sự thay đổi của x sẽ tác động đến việc thay đổi của y như thế nào. Tương ứng với công thức dy/dx.
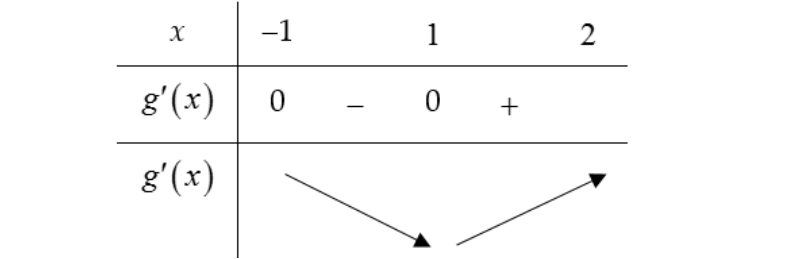
Lúc này bạn có thể hiểu rằng, sự thay đổi của y sẽ phụ thuộc hoàn toàn đến sự thay đổi của biến x.
Vậy nên, giả sử ta có một hàm số y = x, lúc này ta áp dụng công thức tính đạo hàm của hàm số này tương ứng là y’ = 1. Điều này có nghĩa là:
-
x tăng lên 1 đơn vị thì y cũng sẽ tăng 1 đơn vị
-
x giảm 1 đơn vị thì y cũng sẽ giảm 1 đơn vị.
Trường hợp thứ hai, giả sử ta có hàm số y = 2x, khi áp dụng công thức đạo hàm của hàm số này ta sẽ được y’=2. Điều này có nghĩa:
-
x tăng 1 đơn vị thì y tăng lên 2 lần x
-
x giảm 1 đơn vị thì y giảm 2 lần x
Qua hai trường hợp trên có thể thấy được x thay đổi thì y cũng sẽ thay đổi.
Còn trường hợp y = c (c chính là hằng số). Lúc này giá trị của y cũng sẽ không thay đổi, cũng như luôn luôn bằng giá trị của hằng số c.
Như lúc ban đầu ta cũng đã đưa ra rằng, bản chất của đạo hàm chính là việc xét mối quan hệ thay đổi của hai đại lượng trên. Nhưng y lại bằng c, nghĩa là không có sự thay đổi, nên sẽ không có mối quan hệ nào.
Chính vì vậy, bất kỳ hằng số nào thì đạo hàm của nó luôn luôn bằng 0.
Đạo hàm tại vị trí 0 có xác định được không?
Trên thực tế đạo hàm tại vị trí 0 có thể xác định được khi áp dụng công thức tính đạo hàm bình thường ngay tại vị trí tương ứng là x = 0 như sau:
Chính vì vậy, khi áp dụng công thức tính đạo hàm của vị trí x = 0 thì kết quả của nó vẫn bằng 0. Điều này cũng khẳng định rõ hơn khi x = 0 thì không làm cho hàm số thay đổi.
Còn khi xét về mặt hình học, đường tiếp tuyến tại vị trí x = 0 cũng được biểu diễn tương ứng với một đường thẳng trùng với trục Ox của hàm số.
|
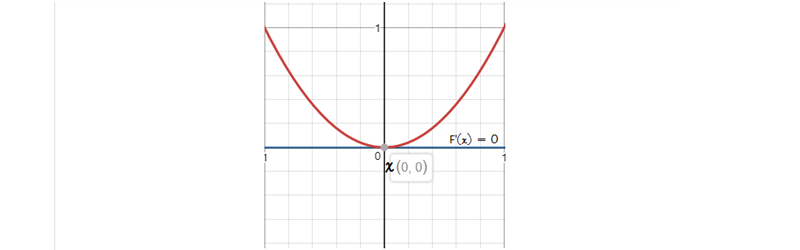
GIÚP CON HỌC TOÁN KẾT HỢP VỚI TIẾNG ANH SIÊU TIẾT KIỆM CHỈ TRÊN MỘT APP MONKEY MATH. VỚI NỘI DUNG DẠY HỌC ĐA PHƯƠNG PHÁP GIÚP BÉ PHÁT TRIỂN TƯ DUY NÃO BỘ VÀ NGÔN NGỮ TOÀN DIỆN CHỈ VỚI KHOẢNG 2K/NGÀY.
|
Một số bài tập về việc chứng minh đạo hàm bằng 0
Dựa vào những kiến thức trên, dưới đây là một số bài tập để các em nhận biết được đâu là hàm số nào khi đạo hàm sẽ bằng 0. Cụ thể:
Xem thêm: Công thức và cách giải bài tập ứng dụng đạo hàm trong vật lý có thể bạn chưa biết!
Kết luận
Trên đây là tổng hợp những thông tin lý giải cho việc tính đạo hàm bằng 0. Qua đó đây là một trong những dạng toán khá ít gặp, nhưng đòi hỏi các em cũng cần phải tìm hiểu kỹ để khi gặp phải cũng có thể giải quyết chính xác.
|
GIẢI PHÁP GIÚP CON PHÁT TRIỂN TOÀN DIỆN TƯ DUY VÀ NGÔN NGỮ VỚI BỘ SẢN PHẨM TOÁN + TIẾNG VIỆT + TIẾNG ANH VỚI ƯU ĐÃI LÊN TỚI 50% NGAY HÔM NAY.
|
Why does the first derivative of a function equal zero, showing the minimum of a function? - Truy cập ngày 17/6/2022
Derivative to Zero, What does it intuitively mean? - Truy cập ngày 17/6/2022
https://math.stackexchange.com/questions/1353453/derivative-to-zero-what-does-it-intuitively-mean
What does it mean that the derivative of a function equals zero? - Truy cập ngày 17/6/2022
![[Giải đáp] Cần ngừng retinol bao lâu trước khi mang thai?](https://vnmedia2.monkeyuni.net/upload/web/storage_web/16-04-2024_11:11:34_ngung-retinol-bao-lau-truoc-khi-mang-thai.png)
![[Giải đáp] Uống củ gai có ảnh hưởng đến thai nhi hay không?](https://vnmedia2.monkeyuni.net/upload/web/storage_web/10-04-2024_16:11:08_uong-cu-gai-co-anh-huong-den-thai-nhi.png)
