Tất tần tật kiến thức về đạo hàm nhiều biến đầy đủ nhất

Đạo hàm nhiều biến là gì?

Giả sử cho D là tập hợp của n số thực tương ứng là x1, x2… xn. Một hàm số thực f trên D được xem là một biểu thức, ứng với mỗi phần tử của D chúng ta sẽ xác định được một giá trị thực tương ứng chính là w = f (x1, x2… xn). Ký hiệu: f : D --> R.

Lúc này, f chính là một hàm số của n, biến số độc lập x1, x2… xn xác định trên D.

Trường hợp hàm hai biến sẽ sử dụng ký hiệu là z = f(x, y).

Tập hợp tất cả những giá trị x1, x2… xn sẽ làm cho biểu thức f có nghĩa được gọi là miền xác định của hàm số f, ký hiệu Df.

Ngoài ra, tương ứng với cặp giá trị (x,y) được xác định trên 1 điểm M(x,y) trên một mặt phẳng Oxy, lúc này miền xác định của hàm số chính là tập hợp những điểm trên mặt phẳng sao cho tại những điểm đó thì hàm số được xác định. Vậy nên, miền xác định của hàm số hai biến thường sẽ được biểu diễn hình học.

Tập hợp những giá trị w được xác định từ hàm số f, được gọi là miền giá trị của hàm số.

Vậy khi đạo hàm của hàm nhiều biến chính là việc tính đạo hàm của hàm số f tương ứng trên miền giá trị của chúng.

Công thức các dạng đạo hàm nhiều biến

Đạo hàm 2 biến trở lên được biết đến là chuyên đề có tính ứng dụng rộng rãi trong những bài toán, vì hầu hết những thuộc tính mà bạn đạo hàm không phải là 1 mà có rất nhiều biến, nhiều tham số. Những tham số này sẽ được liên kết một cách đặc biệt bởi nhiều hàm số khác nhau, thông qua những công thức riêng để tìm được kết quả mong muốn.

Vậy nên, dưới đây là những công thức các dạng đạo hàm của hàm số nhiều biến để các em có thể làm quen và áp dụng:

Giới hạn và liên tục

Đạo hàm riêng

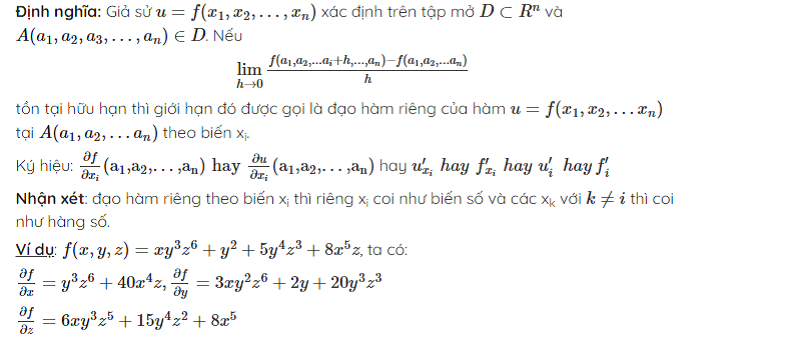
Đạo hàm của hàm hợp nhiều biến

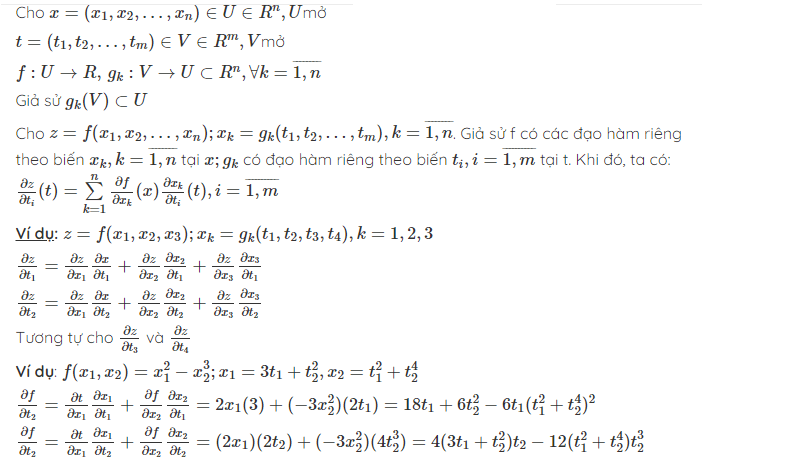
Vi phân đạo hàm nhiều biến

Đạo hàm hàm số nhiều biến riêng cấp cao và vi phân cấp cao

Các bài viết không thể bỏ lỡ

Học toán song ngữ với đa phương pháp cùng Monkey Math chỉ 2K/ngày

Tất tận tật kiến thức về đạo hàm căn: Căn bậc 3, căn u, căn x, căn logarit,...

Đạo hàm và ứng dụng của đạo hàm trong thực tiễn có gì thú vị?

Một số bài tập tự luyện về đạo hàm nhiều biến số từ cơ bản đến nâng cao

Ngoài việc ghi nhớ được lý thuyết, công thức tính đạo hàm hàm nhiều biến, đòi hỏi các em học sinh cần phải kết hợp với thực hành mới hiểu và làm được bài tập.

Vậy nên, dưới đây là một số bài tập liên quan mà Monkey tổng hợp để các em có thể tham khảo và chinh phục nhé:

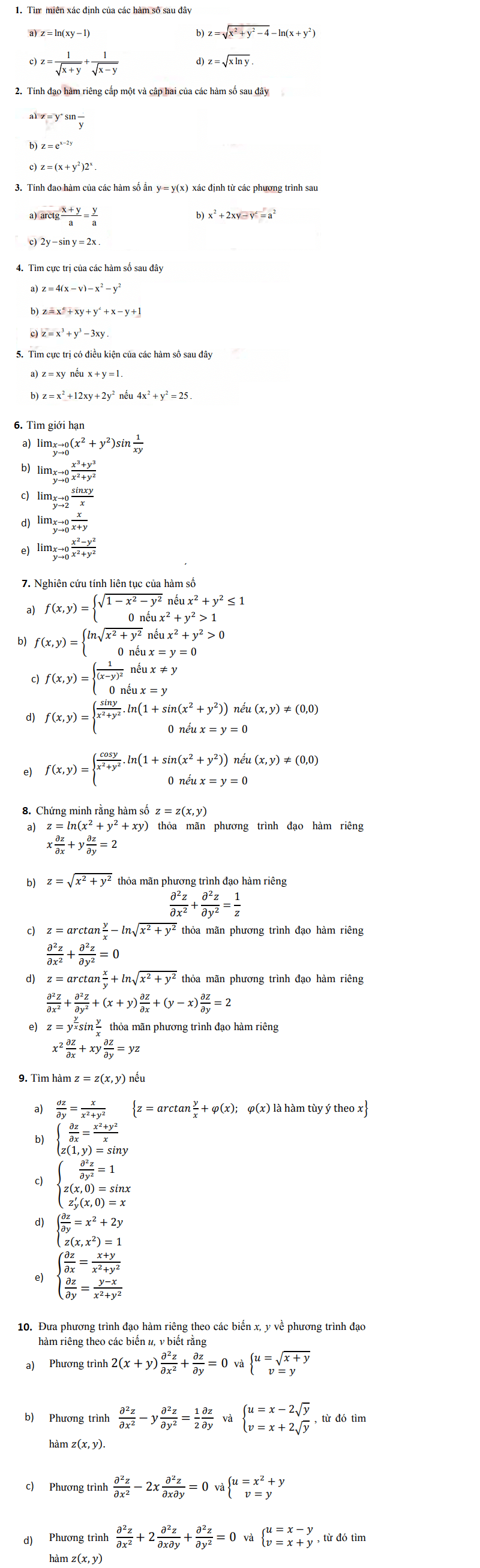
Bí quyết học đạo hàm của hàm nhiều biến hiệu quả hơn

Về cơ bản, chương đạo hàm chủ yếu là những kiến thức khá khó đòi hỏi các em phải nắm vững lý thuyết cho đến thực hành. Bên cạnh đó, để có thể chinh phục dạng toán đạo hàm riêng của hàm nhiều biến hiệu quả hơn, mọi người có thể áp dụng một số bí quyết sau:

• Chia nhỏ kiến thức để học: Thay vì học một lần các dạng công thực đạo hàm nhiều biến trên, các em nên chia nhỏ từng cái để học, khi học kỹ cái này rồi mới đến cái kia để đảm bảo cái nào cũng nắm chắc.
• Thực hành liên tục: Chỉ khi học đi đôi với hành mới đảm bảo các em ghi nhớ lâu hơn, cũng như nhận diện được dạng bài tập để áp dụng công thức đúng và chính xác nhất.
• Áp dụng những chiêu tính đạo hàm bằng máy tính bỏ túi: Hiện nay các dòng máy tính bỏ túi phiên bản mới của Casio Fx 570+, Fx 590,… đều hỗ trợ tính đạo hàm, nên các em có thể tận dụng để tính toán nhanh chóng hơn.

Xem thêm: Công thức đạo hàm nguyên hàm và những kiến thức cần nhớ muốn giải toán chính xác

Kết luận

Trên đây là tổng hợp những kiến thức về đạo hàm nhiều biến. Nhìn chung, đây là một dạng của đạo hàm, nên các em khi nắm vững được kiến thức của đạo hàm cũng sẽ dễ dàng chinh phục dạng toàn này hơn. Chúc các em thành công.