Tỉ số phần trăm là một phần kiến thức toán học mà bất kỳ học sinh não cũng sẽ được học, làm quen và giải bài tập. Tuy nhiên, để giải bài tập đòi hỏi học sinh phải nắm rõ kiến thức công thức và cách tính. Vậy nên, trong nội dung bài viết sau đây Monkey sẽ phân tích chi tiết nhất.
- Khởi đầu tốt nhất cho con bắt đầu học tiếng Anh. Con học càng sớm càng có lợi thế.
- Tích lũy 1000+ từ vựng mỗi năm và 6000 mẫu câu tiếng Anh trước 10 tuổi.
- Linh hoạt sử dụng trên nhiều thiết bị.
- Thành thạo các kỹ năng tiếng Anh ngay trước 10 tuổi với hơn 1000 đầu truyện, hơn 100 bài học, 300+ sách nói. Nội dung thêm mới mỗi tuần.
- Hơn 1.000 đầu truyện, hơn 300 bài học, gần 300 sách nói - thêm mới mỗi tuần.
- Phát âm chuẩn ngay từ đầu nhờ Monkey Phonics - giúp đánh vần tiếng Anh dễ như tiếng Việt.
- Đánh vần chuẩn nhờ học phần Học Vần - cập nhật theo chương trình mới nhất của Bộ GD&ĐT.
- Đọc - hiểu, chính tả tiếng Việt dễ dàng và nhẹ nhàng hơn ngay tại nhà.
- Bồi dưỡng trí tuệ cảm xúc (EQ) nhờ hơn 450 câu chuyện thuộc 11 chủ đề, nhiều thể loại truyện.
Tỉ số phần trăm là gì?
Tỷ số của hai số được biết đến chính là phân số, là thương của phép chia số a cho b (b khác 0). Ký hiệu a/b hoặc a : b.
Tỉ số phần trăm chính là tỉ số của hai số mà ở đây, ta sẽ phải thực hiện quy đồng mẫu số của những tỉ số đó về 100. Ký hiệu: %.
Ví dụ: 50% tương đương với 50/100, hoặc là 0.5. Đọc là năm mươi phần trăm.
Ngoài ra, tỉ số phần trăm thường được ứng dụng để biểu thị độ lớn tương ứng của một lượng này với lượng kia. Ví dụ: 1/100=1%, 25/100=25%
Để có thể biểu diễn được tỉ số phần trăm của một số a, với a là số thập phân hoặc số tự nhiên, ta có a : 100 hoặc a/100 = a%
Ví dụ: 15/100 = 15%
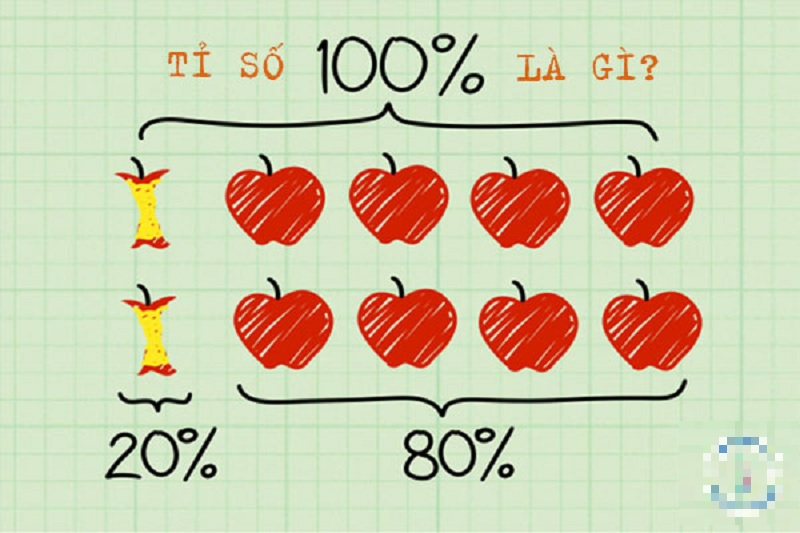
Ý nghĩa của tỉ số phần trăm
Trong toán học, phần trăm tỉ số thực chất chính là phân số với mẫu số là 100. Chúng được sử dụng để biểu thị mức độ lớn tương đối của lượng này so với lượng kia. Cụ thể, đại lượng đầu tiên sẽ thể hiện phần tương ứng hoặc phần thay đổi so với đại lượng thứ hai.
Ví dụ: Một số tiền 50.000 đồng sau khi lãi tăng thêm 3.800 đồng, như vậy số tiền tăng lên một phần bằng 3.800 / 50.000 = 0,076 lần số tiền ban đầu. Nếu diễn đạt theo phần trăm, ta nói số tiền 50.000 đồng đã lãi thêm 7,6%.
Các công thức tính tỉ số phần trăm chi tiết
Để có thể chinh phục được các bài tập khi học toán tỷ số phần trăm, các em cần phải nắm chắc các cách tính tỷ số phần trăm trong từng trường hợp sau đây:
Công thức tính phần trăm giữa 2 số
Để có thể tính được phần trăm tỉ số của A và B, ta tiến hành lấy A chia B rồi nhân 100 rồi thêm ký hiệu % vào kết quả.
Cụ thể:
A / B x 100%
Thực chất, giá trị của việc nhân thêm 100% không thay đổi so với chia A và B. Bởi vì, khi nhân 100% nghĩa là x 100/100 tức là x 1. Vậy nên, nếu ghi thêm ký hiệu % thì người đọc sẽ thầm hiểu được rằng giá trị thực của tỷ số A/B phải lấy phần số không có ký hiệu % chia cho 100.
Ví dụ: Một bó hoa có 25 bông hoa, trong đó có 6 bông hoa vàng. Tìm tỉ số phần trăm của bông hoa vàng so với tổng số bông hoa?
Cách giải:
Xem A là 25 bông hoa tổng cộng, số B là 6 bông hoa vàng. Tỉ số phần trăm của bông hoa vàng trong bó hoa là:
(6 : 25) x 100 = 24%
Đáp số: 24% bông hoa vàng
Công thức tính tỉ số % của một số
Muốn tìm phần trăm của một số, ta sẽ tiến hành lấy số đó chia cho 100, rồi tiếp tục nhân với số % hoặc lấy số đó nhân với số % rồi chia cho 100.
Cụ thể:
A x a% = A : 100 x a
Ví dụ: Một cuộn vải dài 300m, thợ may cắt được 30% chiều dài của cuộn vải đó. Hỏi phần còn lại của cuộn vải mà thợ may cần phải cắt là bao nhiêu?
Cách giải:
Cuộn vải đã cắt được: 30% x 300 = 90 mét
Phần vải còn lại cần phải cắt là: 300 - 90 = 210 mét
Đáp số: 210 mét vải.
Công thức tìm một số khi biết phần trăm của số đó
Nếu đề bài cho biết phần trăm của một số và đi tìm giá trị của số đó, ta sẽ tiến hành lấy số đó chia cho số phần trăm rồi nhân 100 hoặc có thể lấy giá trị đó nhân 100 và chia cho số phần trăm đã biết.
Cụ thể, muốn tìm một số biết b% của số đó là B:
B : b% = B : b x 100
Công thức này sẽ ngược lại với công thức tìm tỷ số % của một số cho trước.
Ví dụ: Một quyển sách đã đọc được 120 trang, chiếm 15% số trang sách. Hỏi cuốn sách đó có bao nhiêu trang?
Cách giải:
Bởi vì 120 trang chiếm 15% số trang sách nên suy ra 1% số trang của quyển sách đó là:
120 : 15% = 8 trang
Vậy số trang sách là: 8 x 100 = 800 trang
Đáp số: 800 trang sách
|
XÂY DỰNG NỀN TẢNG TOÁN HỌC VỮNG CHẮC CHO TRẺ TỪ NHỎ VỚI ĐA PHƯƠNG PHÁP DẠY HỌC TÍCH CỰC, CHI PHÍ CỰC RẺ CHƯA ĐẾN 2K/NGÀY CÙNG MONKEY MATH.
|
Các dạng bài tập tính tỷ số phần trăm thường gặp và phương pháp giải
Trong chương trình toán tiểu học, các em sẽ được làm quen với kiến thức tỉ số phần trăm. Cùng với đó, học sinh sẽ được học và phải chinh phục các dạng bài tập sau:
Dạng 1: Bài toán về cộng, trừ, nhân, chia tỉ số phần trăm
Để giải được các bài tập về các phép tính tỉ số %, ta áp dụng những công thức sau:
Công thức toán cộng: a% + b% = (a + b)%.
Ví dụ: 5% + 12% = (5 + 12)% = 18%
Công thức toán trừ a% - b% = (a - b)%.
Ví dụ: 42% - 8% = (42 - 8)% = 34%
Công thức toán nhân a% × b = (a × b)%.
Ví dụ: 5% × 7 = (5 × 7)% = 35%
Công thức toán chia a% : b = (a : b)%
Ví dụ: 27% : 9 = (27 : 9) = 3%
Dạng 2: Tìm tỉ số phần trăm của hai số
Phương pháp giải: Với dạng bài tập này, các em sẽ chỉ áp dụng công thức tìm tỷ số % của cả hai số đã đưa ra phía trên, rồi làm theo hướng dẫn và đưa ra đáp án chính xác.
Ví dụ: Một cửa hàng đặt kế hoạch tháng này bán được 12 tấn gạo, nhưng thực tế cửa hàng bán được 15 tấn gạo. Hỏi:
a. Cửa hàng đã thực hiện được bao nhiêu phần trăm kế hoạch?
b. Cửa hàng đã vượt mức kế hoạch bao nhiêu phần trăm?
Hướng dẫn giải:
a. Cửa hàng đã thực hiện được so với kế hoạch là: (15 : 12) x 100 = 125% (kế hoạch)
b. Cửa hàng đã vượt mức kế hoạch là: 125% - 100% = 25% (kế hoạch)
Đáp số:
a. 125% kế hoạch
b. 25% kế hoạch
Dạng 3: Tìm phần trăm của một số
Phương pháp giải: Các em cũng sẽ áp dụng công thức lấy số đó chia cho 100 rồi nhân với số %, hoặc lấy số đã cho nhân với số % rồi chia cho 100 để có thể tính được giá trị % của một số tương ứng chính xác.
Ví dụ: Lớp 5A có 30 học sinh trong đó số học sinh nữ chiếm 60%. Hỏi số học sinh nữ có bao nhiêu em.
Hướng dẫn giải:
Số học sinh những của lớp 5A là: 30 : 100 x 60 = 18 (học sinh)
Đáp số: 18 (học sinh nữ)
Dạng 4: Tìm một số khi biết giá trị phần trăm của số đó
Phương pháp giải: Để tính được giá trị một số khi biết được số % của số đó thì ta tiến hành lấy giá trị đó chia cho số % rồi nhân 100, hoặc có thể lấy giá trị đã cho nhân 100 và chia cho số % đã biết.
Ví dụ: Một lớp có 25% học sinh giỏi, 55% học sinh khá còn lại là học sinh trung bình. Tính số học sinh của lớp đó biết số học sinh trung bình là 5 bạn?
Hướng dẫn giải:
Nếu xem tổng số học sinh của lớp là 100% thì số học sinh trung bình so với số học sinh của lớp là:
100% - (25% + 55%) = 20%
Số học sinh của lớp là:
5 : 20 x 100 = 25 (học sinh)
Đáp số: 25 học sinh
Dạng 5: Bài toán về tính lãi, tính vốn
Phương pháp giải: Để tính được lãi và vốn bỏ ra chiếm bao nhiêu phần trăm, ta lấy % giá bán chia cho % giá mua.
Ví dụ: Một cửa hàng định giá mua hàng bằng 75% giá bán. Hỏi cửa hàng đó định giá bán bằng bao nhiêu phần trăm giá mua?
Hướng dẫn giải
Xem giá bán là 100% thì giá mua là 75%.
Vậy giá bán ra so với giá mua vào chiếm số phần trăm là: 100 : 75 = 133,33%
Đáp số: 133,33% giá mua
Dạng 6: Bài toán đưa về dạng toán quen thuộc
Phương pháp giải: Với dạng bài tập này, học sinh sẽ đưa dạng toán về những dạng quen thuộc như tổng – tỉ, hiệu – tỉ,... để tìm ra đáp án chính xác, nhanh chóng hơn.
Ví dụ: Tổng của hai số bằng 25% thương của hai số đó cũng bằng 25%. Tìm hai số đó.
Hướng dẫn giải:
25% = 0,25
Số thứ nhất là: 0,25 : (1+4) = 0,05
Số thứ hai là: 0,25 – 0,05 = 0,2
Đáp số: 0,05 và 0,2
Tổng hợp các dạng toán lớp 5 tỉ số phần trăm và hướng dẫn cách làm chi tiết
Phép nhân phân số: Quy tắc, bài tập và hướng dẫn giải chi tiết nhất
Quy trình giải toán phép cộng phân số từng bước chi tiết nhất
Bài tập tính tỉ số phần trăm để học sinh luyện tập
Sau khi đã nắm chắc được lý thuyết của kiến thức tỷ số phần trăm, chắc hẳn các em cũng đã yên tâm hơn trong việc chinh phục các bài tập liên quan. Vậy nên, dưới đây Monkey sẽ tổng hợp một số bài tập, câu hỏi để các em cùng nhau luyện tập nhé.
Câu 1: Một lớp học có 28 bạn, trong đó có 7 bạn nam. Hãy tìm tỉ số phần trăm học sinh nam so với sĩ số của lớp?
Câu 2: Trong chuồng gà có 12 con gà mái và 28 con gà trống. Tìm tỉ số phần trăm số gà mái so với số gà trong vườn?
Câu 3: Diện tích của một vườn hoa là 100m2, trong đó 35m2 trồng hoa ly. Tìm tỉ số diện tích trồng hoa ly và diện tích vườn hoa.
Câu 4: Vòi nước thứ nhất mỗi giờ chảy vào được 1/6 thể tích của bể, vòi nước thứ hai mỗi giờ chảy vào được 1/3 thể tích của bể. Hỏi cả hai vòi nước cùng chảy vào bể trong một giờ thì được bao nhiêu phần trăm thể tích của bể?
Câu 5: Chiếc xe đã đi được 40% chiều dài của con đường dài 250 km. Tính chiều dài quãng đường mà xe đã đi.
Câu 6: Số học sinh giỏi của một trường tiểu học là 64 em chiếm 12,8 % số học sinh toàn trường. Hỏi trường đó có bao nhiêu học sinh?
Câu 7: Một người bỏ ra 42000đ tiền vốn để mua rau. Sau khi bán hết số rau, người đó thu được 52500đ.
a.Tiền bán rau bằng bao nhiêu phần trăm tiền vốn?
b.Người đó thu lãi bao nhiêu phần trăm?
Câu 8: Một sản phẩm đã hạ giá bán 20% hỏi muốn bán sản phẩm đó với giá ban đầu thì phải tăng giá thêm bao nhiêu phần trăm?
Câu 9: Cô giáo đem chia táo cho học sinh. Nếu mỗi em 9 quả thì thiếu 9 quả. Nếu chia mỗi em 10 quả thì thiếu 25% số táo ban đầu. Tính số táo cô đem chia và số học sinh được chia táo.
Câu 10: Một người đem trứng đi bán: buổi sáng bán được 50% số trứng, buổi chiều bán được 20% số trứng còn lại. Sau đó người đó lại buôn thêm 40 quả nữa. Tối về người đó lại thấy rằng số trứng đem về bằng 120% số trứng mang đi. Hỏi người ấy mang đi mấy quả trứng?
Câu 11: Lượng muối chứa trong nước biển là 5%. Cần phải đổ thêm vào 200kg nước biển bao nhiêu kg nước lã để được một loại dung dịch chứa 2% muối?
Câu 12: Trong trường có 68% số học sinh biết tiếng Nga, 5% biết cả tiếng Anh lẫn tiếng Nga. Số còn lại chỉ biết tiếng Anh. Hỏi có bao nhiêu phần trăm số học sinh trong trường biết tiếng Anh?
Câu 13: Nhân ngày 26-3, một cửa hàng bán đồ lưu niệm bán hạ giá 10% so với ngày thường. Tuy vậy họ vẫn lãi 8% so với giá vốn. Hỏi ngày thường họ lãi bao nhiêu phần trăm so với giá vốn?
Câu 14: Một cửa hàng buôn bán hoa quả đặt hàng 4,5 tấn cam với giá 18000 đồng một kilôgam. Tiền vận chuyển là 1 600 000 đồng. Giả sử 10% số cam bị hỏng trong quá trình vận chuyển và tất cả số cam đều bán được. Hãy tính xem mỗi kg cam cần bán với giá bao nhiêu để thu lãi 8%?
Câu 15: Bố mua 2 đôi giày cho Hùng nhưng đều bị nhỏ nên mẹ phải mang bán 2 đôi giày đó đi. Mỗi đôi giày đều bán với giá 300.000 đồng. Trong đó một đôi bán nhiều hơn giá mua 20%, đôi kia bán ít hơn giá mua 20%. Hỏi mẹ Tiến bán được lãi hay lỗ bao nhiêu tiền?
|
GIẢI PHÁP GIÚP CON PHÁT TRIỂN TOÀN DIỆN TƯ DUY VÀ NGÔN NGỮ VỚI BỘ SẢN PHẨM TOÁN + TIẾNG VIỆT + TIẾNG ANH VỚI ƯU ĐÃI LÊN TỚI 50% NGAY HÔM NAY.
|
Ứng dụng công thức tính tỉ số phần trăm vào thực tiễn
Công thức tính tỉ số phần trăm là một công thức toán học đơn giản nhưng có thể ứng dụng rộng rãi trong thực tiễn. Cụ thể như:
- Trong lĩnh vực kinh tế - tài chính, tỉ số phần trăm được sử dụng để tính toán lãi suất, thuế, doanh thu, chi phí, lợi nhuận,... Ví dụ: Lãi suất ngân hàng được tính theo tỉ lệ phần trăm trên số tiền gửi.
- Trong lĩnh vực giáo dục, tỉ số phần trăm được sử dụng để tính điểm thi, điểm trung bình, xếp loại học sinh,... Ví dụ: Điểm thi của một học sinh được tính bằng tổng số điểm đạt được chia cho tổng số điểm tối đa.
- Trong lĩnh vực y tế, tỉ số phần trăm được sử dụng để tính tỷ lệ mắc bệnh, tỷ lệ tử vong,... Ví dụ: Tỷ lệ mắc bệnh được tính bằng số người mắc bệnh chia cho tổng số người trong một cộng đồng.
- Trong lĩnh vực khoa học, tỉ số phần trăm được sử dụng để tính hàm lượng của một chất trong một hỗn hợp,... Ví dụ: Hàm lượng nước trong một quả cam được tính bằng khối lượng nước chia cho khối lượng tổng thể của quả cam.
Kết luận
Trên đây là những thông tin chia sẻ về kiến thức tỉ số phần trăm, một trong những dạng toán cơ bản trong toán học, cũng như tính ứng dụng thực tiễn rất cao. Vậy nên, phụ huynh có thể nắm vững những kiến thức này để hỗ trợ công việc, cũng như giúp hướng dẫn con trẻ học tập và chinh phục dạng bài tập này tốt hơn nhé.
![[Giải đáp] Cần ngừng retinol bao lâu trước khi mang thai?](https://vnmedia2.monkeyuni.net/upload/web/storage_web/16-04-2024_11:11:34_ngung-retinol-bao-lau-truoc-khi-mang-thai.png)
