Trong số các phần chuyên đề toán học ôn thi THPT Quốc Gia môn Toán, chuyên đề Xác suất - Tổ hợp thường được đánh giá là có tính chất trừu tượng và khó khăn, khiến nhiều học sinh cảm thấy hoang mang và lo lắng. Hiểu được điều này, Monkey đã tổng hợp những phương pháp học tập hiệu quả và các tài liệu ôn tập được chọn lọc kỹ càng để chia sẻ ngay trong bài viết sau.
.png)
Chuyên đề tổ hợp xác suất trong cấu trúc đề thi Toán THPT Quốc Gia 2024
Cấu trúc đề thi Toán THPT Quốc Gia 2024 bao gồm 50 câu hỏi, 45 câu thuộc về kiến thức lớp 12 và 5 câu liên quan đến lớp 11. Trong đó, chuyên đề tổ hợp xác suất chiếm 2 câu trên tổng số 50 câu hỏi, và độ khó ở mức trung bình (gồm: 1 câu thông hiểu và 1 câu vận dụng). Thế nên, để đạt được số điểm cao môn toán, các thí sinh không nên chủ quan mà bỏ qua việc ôn tập tổ hợp xác suất.
Ôn tập lý thuyết về chuyên đề xác suất - tổ hợp
Dưới đây là phần tóm tắt lý thuyết quan trọng về chuyên đề tổ hợp xác suất ôn thi Đại Học.
Quy tắc cộng - Quy tắc nhân
Quy tắc cộng là gì? Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m + n cách thực hiện.
Quy tắc nhân là gì? Một công việc được hoành thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.
Hoán vị, chỉnh hợp, tổ hợp
1. Hoán vị
Định nghĩa: Cho tập hợp A gồm n phần tử (n ≥ 1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập A được gọi là một hoán vị của n phần tử đó.
Định lí: Pn = n(n - 1)...2.1 = n!
Quy ước: 0! = 1
2. Chỉnh hợp
Định nghĩa: Cho tập A gồm n phần tử (n ≥ 1). Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
Định lí:
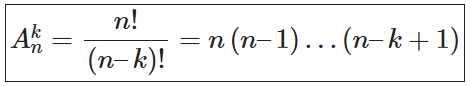
3. Tổ hợp
Định nghĩa: Giả sử tập A có n phần tử (n ≥ 1). Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.
Định lí:
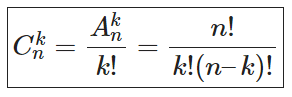
Tính chất:
- Cho số nguyên dương n và số nguyên k với 0 ⩽ k ⩽ n. Khi đó:
- Cho số nguyên dương n và số nguyên k với 1 ⩽ k ⩽ n. Khi đó:
Quy ước: Tổ hợp chập 0 của n phần tử là tập rỗng.
Xác suất của biến cố
Giả sử một phép thử có không gian mẫu Ω gồm hữu hạn các kết quả có cùng khả năng xảy ra và A là một biến cố.
Xác suất của biến cố A là một số, kí hiệu là P(A), được xác định bởi công thức:
P(A) = n(A) / n(Ω) = |ΩA| / |Ω|
Trong đó: n(A) và n(Ω) lần lượt là ký hiệu số phần tử của tập A và Ω.
Lưu ý:
- 0 ⩽ P(A) ⩽ 1.
- P(Ω) = 1, P(∅) = 0.
- Cho A là một biến cố. Khi đó biến cố “Không xảy ra A”, kí hiệu là Ā, được gọi là biến cố đối của A. Với Ā = Ω \ A; P(Ā) + P(A) = 1 ⇒ P(Ā) = 1 - P(A).

Các dạng bài tập tổ hợp - xác suất ôn thi THPT Quốc Gia
Như vậy, sau khi đã hiểu rõ về các lý thuyết thuộc chuyên đề về tổ hợp xác suất, các thí sinh cần luyện tập thành thạo 2 dạng toán quan trọng thuộc chuyên đề xác suất ôn thi THPT Quốc Gia như sau:
Dạng 1: Tìm số hoán vị, chỉnh hợp, tổ hợp
Ví dụ 1: Cho tập hợp M có 10 phần tử. Số tập con gồm hai phần từ của M là bao nhiêu?
Mỗi cách lấy ra 2 phần tử trong 10 phần tử của M để tạo thành tập con gồm 2 phần tử là một tổ hợp chập 2 của 10 phần tử ⇒ Số tập con của M gồm 2 phần tử là C102.
Ví dụ 2: Một tổ có 7 học sinh nam và 5 học sinh nữ. Hỏi có bao nhiêu cách chọn ra 6 học sinh trong đó có đúng 2 học sinh nữ?
Chọn ra 6 học sinh trong đó có đúng 2 học sinh nữ nên có 4 học sinh nam. Vậy số cách chọn là: C74.C52 = 350.
Dạng 2: Tính xác suất của biến cố
Ví dụ 1: Một đoàn đại biểu gồm 5 người được chọn ra từ một tổ gồm 8 nam và 7 nữ để tham dự hội nghị. Xác suất để chọn được đoàn đại biểu có đúng 2 người nữ là bao nhiêu?
Số phần tử của không gian mẫu: n(Ω) = C155.
Gọi biến cố A là “Chọn được đoàn đại biểu có đúng 2 người nữ”.
⇒ n(A) = C72.C83.
Vậy xác suất cần tìm là P(A) = n(A) / n(Ω) = 56/143.
Ví dụ 2: Một hộp đựng 5 viên bi đỏ, 4 viên bi xanh. Lấy ngẫu nhiên 3 viên bi từ hộp đó. Tính xác suất lấy được ít nhất 1 viên đỏ.
Lấy 3 viên bi từ 5 + 4 = 9 viên bi có C93 cách.
Lấy 1 viên bi đỏ và 2 viên bi xanh có C51.C42 cách.
Lấy 2 viên bi đỏ và 1 viên bi xanh có C52.C41 cách.
Lấy 3 viên bi đỏ có C53 cách.
Vậy xác suất cần tìm là [C51.C42 + C52.C41 + C53] / C93 = 20/21.
40+ Bài tập tổ hợp xác suất thi THPT Quốc Gia (có đáp án)
Tham khảo một số dạng bài tập xác suất ôn thi THPT Quốc Gia theo từng mức độ từ dễ đến nâng cao do Monkey tổng hợp và chọn lọc ngay dưới đây!
Bài tập chuyên đề xác suất tổ hợp mức độ nhận biết

|
ĐÁP ÁN |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
C |
D |
B |
D |
A |
C |
B |
A |
B |
Bài tập chuyên đề xác suất tổ hợp mức độ thông hiểu

|
ĐÁP ÁN |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
A |
C |
D |
B |
C |
C |
A |
A |
C |
A |
Bài tập chuyên đề tổ hợp xác suất vận dụng thấp

|
ĐÁP ÁN |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
D |
B |
D |
D |
C |
D |
A |
A |
C |
C |
Bài tập chuyên đề tổ hợp xác suất vận dụng cao

|
ĐÁP ÁN |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
D |
A |
C |
A |
A |
A |
D |
D |
A |
B |
Xem thêm:
Với những kiến thức và phương pháp học tập được chia sẻ trong bài viết này, hy vọng các bạn học sinh đã có thêm niềm tin và động lực để chinh phục chuyên đề Xác suất - Tổ hợp trong kỳ thi THPT Quốc Gia môn Toán sắp tới. Hãy nhớ rằng, chìa khóa thành công nằm ở sự nỗ lực và kiên trì của mỗi cá nhân. Chúc các bạn học tập hiệu quả và đạt được kết quả cao trong kỳ thi!







.png)
.png)









.png)