.png)
Rút gọn phân số hay còn gọi là tìm phân số tối giản là dạng bài tập thường gặp trong chương trình toán lớp 4, cũng như các lớp cao hơn. Vậy nên, để nắm được phương pháp tối giản phân số nhanh chóng, chính xác thì Monkey sẽ chia sẻ ngay những cách sau đây.
Rút gọn phân số là gì?
Rút gọn phân số hay còn gọi là tối giản phân số, đây là phân số mà có tử và mẫu số không thể cùng chia hết cho số nào ngoài trừ 1 (hoặc -1 nếu là các số âm). Nói dễ hiểu, phân số a/b là tối giản nếu cả a và b đều là số nguyên tố cùng nhau, hay là chúng có ước số chung lớn nhất là 1.
Ví dụ: 1/5; 15/29; 11/12;… sẽ là những phân số tối giản.
Các cách tìm phân số tối giản chi tiết
Trong cách rút gọn phân số nhanh nhất, ta sẽ tiến hành chia cả tử và mẫu số cho cùng 1 số đảm bảo số bị khác khác 0 và 1. Ngoài ra, các em cũng có thể tối giản phân số theo các cách sau đây.
Cách 1: Sử dụng thừa số chung lớn nhất
Bước 1: Liệt kê các thừa số của cả tử và mẫu số từ nhỏ đến lớn, bao gồm cả 1 hoặc chính nó. Thừa số ở đây chính là số mà khi bạn nhân chúng với nhau sẽ được số khác, ví dụ 2 và 5 là hai thừa số của 10, vì ta có thể nhân chúng lại với nhau để có kết quả là 10.
Ví dụ, liệt kê thừa số chung của phân số 24/32:
24: 1, 2, 3, 4, 6, 8, 12, 24.
32: 1, 2, 4, 8, 16, 32.
Bước 2: Tìm thừa số chung lớn nhất (GCF) của tử và mẫu số. GCF chính là số lớn nhất mà các số có thể đều chia hết. Sau khi đã tìm và liệt kê các thừa số ở bước 1, sau đó bạn phải tìm ra GCF của hai số đó.
Chẳng hạn:
24: 1, 2, 3, 4, 6, 8, 12, 24.
32: 1, 2, 4, 8, 16, 32.
Lúc này GCF của 24 và 32 là 8, vì 8 là số lớn nhất mà cả 24 và 32 đều chia hết cho.
Bước 3: Tiến hành chia và tử và mẫu cho GCF. Sau khi đã tìm được GCF ở bước 2, ta tiến hành chia cả tử và mẫu số cho số đó để đưa chúng về phân số tối giản.
Ta có:
24/8 = 3
32/8 = 4
Lúc này phân số được rút gọn là 3/4.
Bước 4: Kiểm tra kết quả. Để chắc chắn hơn việc phân số đã được rút gọn, mọi người tiến hành kiểm tra bằng cách nhân nhân tử và mẫu số vừa rút gọn cho GCF, nếu ra kết quả phân số ban đầu thì chính xác.
Cụ thể:
3 * 8 = 24
4 * 8 = 32
Lúc này, kết quả chính là phân số ban đầu 24/32.
Cách 2: Mẹo rút gọn phân số lớp 4 bằng cách chia liên tiếp cho một số nhỏ
Bước 1: Lựa chọn một số nhỏ. Cụ thể, ở cách rút gọn phân số này các em sẽ chọn một chữ số nhỏ như 2, 3, 4… để bắt đầu. Nhìn xem phần tử và mẫu số có chia được hết ít nhất một lần cho số mà bé đã chọn hay không.
Ví dụ, phân số 24/32, số 2 là thích hợp nhất vì cả 24 và 32 đều là số chẵn, có thể chia hết cho 2.
Bước 2: Chia cả tử và mẫu số cho số nhỏ nhất đã chọn. Sau khi đã tìm được số nhỏ nhất để chia ở bước 1, ta tiến hành chia cả tử và mẫu cho số đó.
Cụ thể:
24/2 = 12
32/2 = 16
Lúc này ta được phân số mới 12/16.
Bước 3: Lặp lại quá trình này. Nếu cả tử và mẫu đều vẫn chia tiếp được cho số nhỏ đã chọn đó, ta tiếp tục thực hiện lại bước 2. Nếu chỉ một hoặc cả 2 là số lẻ thì sẽ phải tìm số nhỏ khác và chia chúng cho số mới đó.
12/2 = 6
16/2 = 8
Phân số mới là 6/8.
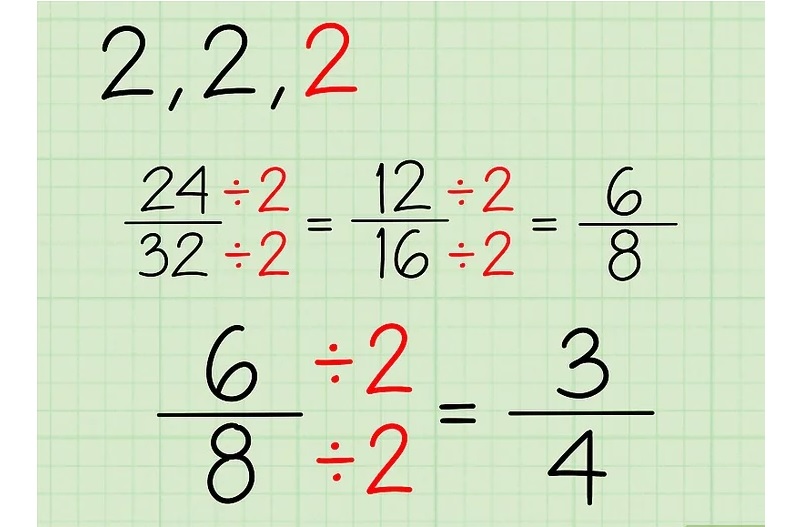
Bước 4: Tiếp tục chia cả tử và mẫu cho số đó cho đến khi không thể chia thêm nữa. Ở đây nếu cả tử và mẫu số mới vẫn là số chẵn, ta tiếp tục chia tiếp cho 2 cho đến khi không thể chia thêm được nữa.
Cụ thể:
6/2 = 3
8/2 = 4
Ta được phân số mới là 3/4.
Bước 5: Hãy đảm bảo phân số mới không thể rút gọn được nữa. Có nghĩa phân số mới đó chỉ có thể chia hết cho 1 và chính nó thì đó là phân số đã được tối giản. Chẳng hạn ở phân số ¾ ta không thể chia hết được cho số nào nữa ngoài trừ nó và 1 thì phân số đã được rút gọn.
Bước 6: Kiểm tra lại kết quả. Ta sẽ nhân ¾ với 2/2 ba lần để xem có ra được kết quả là phân số ban đầu là 24/32 không nhé.
Cụ thể:
3/4 * 2/2 = 6/8
6/8 * 2/2 = 12/16
12/16 * 2/2 = 24/32.
Lưu ý: Các em đã chia 24/32 cho 3 lần 2 có nghĩa là 2 x 2 x 2 tương ứng với việc chia nó cho 8, đây chính là GCF của cả tử và mẫu. Đây là cách rút gọn phân số khá rườm rà hơn với cách 1, nhưng sẽ giúp các bé hiểu được bản chất khi thực hiện phép tính.
Cách 3: Cách rút gọn phân số lớp 4 bằng cách liệt kê các thừa số
Bước 1: Viết ra phân số cần rút gọn. Phần này các em hãy để một khoảng trống bên phải để viết ra các thừa số.
Bước 2: Tiến hành liệt kê các thừa số của các tử và mẫu. Bắt đầu từ 1 và những thừa số tiếp theo sẽ liệt kê thành từng cặp.
Chẳng hạn: Cho phân số 24/60
Thừa số 24: 1, 2, 3, 4, 6, 8, 12, 24
Thừa số 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Bước 3: Chọn và chia cả tử và mẫu cho thừa số chung lớn nhất. Trong danh sách các thừa số đã tìm ở bước 2, các em tiến hành chọn số lớn nhất xuất hiện ở trong các thừa số của cả tử và mẫu số cho số đó.
Như ví dụ trên, ta thấy cả tử và mẫu có GCF chính là 12. Lúc này, ta sẽ chia 24 cho 12 và 60 chia 12. Lúc này kết quả là 2/5 là phân số đã được rút gọn.
Cách 4: Cách rút gọn phân số tối giản sử dụng sơ đồ cây thừa số nguyên tố
Bước 1: Tìm thừa số nguyên số của tử và mẫu số của phân số. Số nguyên tố chính là số không chia được cho số nào khác ngoài 1 và chính nó như 2, 3, 5, 7, 11.
Cũng ở ví dụ 24/60.
Đầu tiên, ta bắt đầu với tử số. Từ 24 chia thành 2 nhánh là 2 và 12 (2 x 12 = 24). Vì 2 là số nguyên tố nên nhánh đó đã hoàn thành. Tiếp tục ở nhánh 12 tách thành 2 số khác là 2 và 6. Tiếp tục 2 là số nguyên tố nên đã xong, giờ tiếp tục tìm số nguyên tố của 6 là 2 và 3. Lúc này ta có nhanh 2, 2, 2 và 3 là các số nguyên tố cần tìm của 24.
Chuyển sang mẫu số là 60. Đầu tiên ta phân nhánh cây thành 2 và 30. Nhánh 2 đã xong, chuyển sang 20 sẽ được 2 và 15. Tiếp tục ở nhánh 15 ta chia thành nhánh 3 và 5, cả hai đều là số nguyên tố. Nên kết quả ta được 2, 2, 3 và 5 là số nguyên tố của 60.
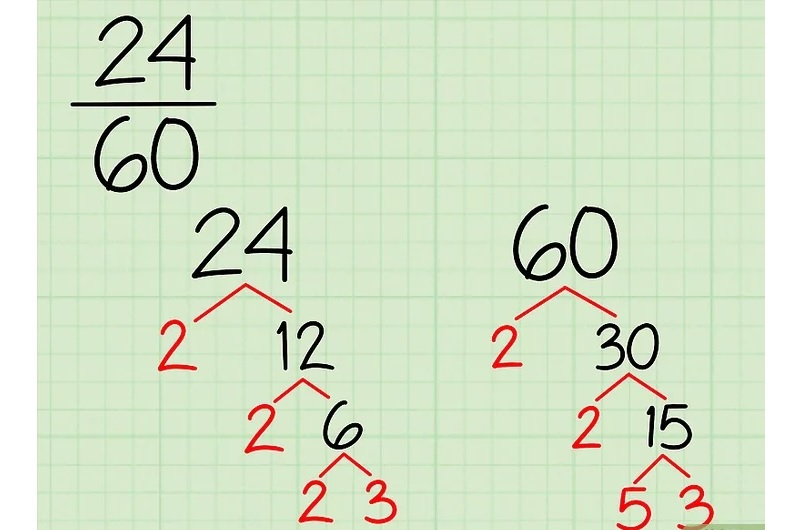
Bước 2: Viết kết quả thành thừa số nguyên tố của tử và mẫu số. Ta sẽ liệt kê các thừa số nguyên tố của cả tử và mẫu, viết chúng dưới dạng phép nhân để kiểm tra kết quả chính xác.
Với 24, ta có 2 x 2 x 2 x 3 = 24.
Với 60, ta có 2 x 2 x 3 x 5 = 60
Bước 3: Gạch bỏ các thừa số chung. Bất kỳ số nào mà xuất hiện ở cả tử và mẫu thì bạn sẽ gạch bỏ. Ở vì dụ trên ta thấy có hai số 2 và một 3 là các số chung nhau. Lúc này ta còn lại 2 và 5 hay 2/5 chính là phân số rút gọn của 24/60.
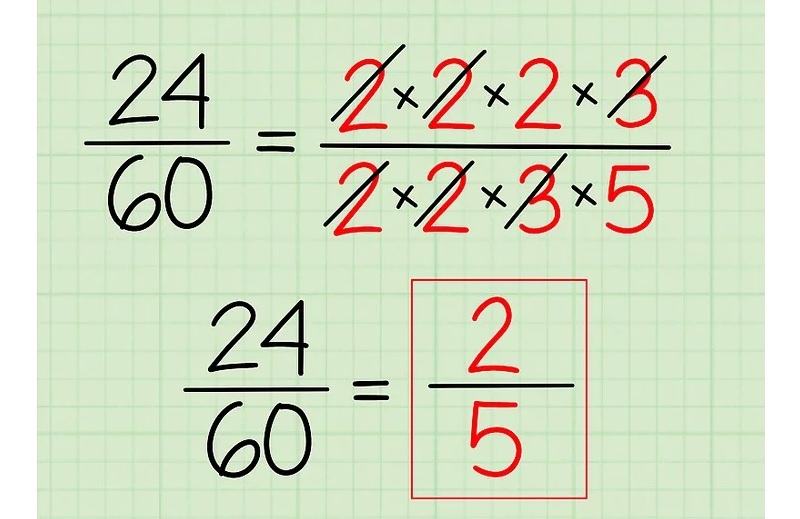
Cách 5: Sử dụng công cụ rút gọn phân số online
Hiện nay có rất nhiều công cụ hỗ trợ rút gọn phân số bài tập tối giản, nhanh chóng, chính xác trên internet để các em tham khảo. Chỉ cần bạn nhập tử số và mẫu số tương ứng thì hệ thống sẽ giúp tính toán nhanh chóng nhất. Chẳng hạn như một số công cụ tại tienichnho.com/rut-gon-phan-so, Giaitoannhanh.com/rut-gon-phan-so/...
|
XÂY DỰNG NỀN TẢNG TOÁN HỌC, PHÁT TRIỂN TƯ DUY NĂNG LỰC HỌC TOÁN VÀ PHÁT TRIỂN NGÔN NGỮ CHO TRẺ CÙNG VỚI MONKEY MATH CHỈ VỚI 2K/NGÀY.
|
Lưu ý khi giải bài tập rút gọn phân số tối giản
Để giải bài toán liên quan đến phân số trong lớp 4 một cách hiệu quả, bạn có thể áp dụng các lưu ý sau:
- Hiểu rõ về phân số: Phân số là phần của một số được chia thành các phần bằng nhau. Nó gồm hai thành phần chính là tử số (phần được chia) và mẫu số (số chia đều phần tử số).
- Rút gọn phân số: Để rút gọn phân số, tìm ước chung lớn nhất của tử số và mẫu số, sau đó chia cả hai cho ước chung đó để đơn giản hóa phân số.
- Cộng và trừ phân số: Để cộng hoặc trừ phân số, cần đồng mẫu số bằng cách tìm bội số chung nhỏ nhất của mẫu số hai phân số. Sau đó, thực hiện phép tính với tử số đã có.
- Nhân và chia phân số: Để nhân phân số, nhân tử số với tử số và mẫu số với mẫu số, rồi rút gọn kết quả nếu cần thiết. Còn để chia phân số, lấy phân số chia nhân với nghịch đảo của phân số chia.
- Xác định phân số tối giản: Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho bất kỳ số tự nhiên nào lớn hơn 1. Ví dụ: 1/2, 3/5, 7/11 là phân số tối giản.
- Trường hợp không thể rút gọn: Nếu không tìm được ƯCLN nào lớn hơn 1 của tử số và mẫu số, thì phân số đó đã ở dạng tối giản.
- Một số mẹo rút gọn phân số nhanh:
- Phân tích tử số và mẫu số thành các thừa số nguyên tố.
- Loại bỏ những thừa số chung xuất hiện ở cả tử số và mẫu số.
- Sử dụng các hằng đẳng thức đáng nhớ, ví dụ: a^2 - b^2 = (a + b)(a - b).
- Khi rút gọn phân số, cần chú ý giữ nguyên giá trị của phân số.
- Tránh mắc các sai lầm như lấy tử số chia cho mẫu số, hoặc ngược lại.
- Nên kiểm tra lại kết quả sau khi rút gọn.
Bài tập rút gọn phân số lớp 4 để học sinh tự luyện
Sau khi nắm được các cách tối giản phân số, dưới đây là một số bài tập để các em cùng nhau luyện tập.
Kết luận
Trên đây là những kiến thức cơ bản về toán rút gọn phân số. Hy vọng dựa vào những chia sẻ trên sẽ giúp các bé có thể hiểu và cùng nhau luyện tập và thực hành hiệu quả nhất.
