Diện tích hình thang cân: Công thức, cách tính và bài tập ví dụ

Trong chương trình toán học, việc hiểu rõ về 'diện tích hình thang cân' là vô cùng quan trọng. Không chỉ là một phần cơ bản trong chương trình học, diện tích hình thang cân còn thường xuất hiện trong các bài toán thực tế và kỳ thi. Để giúp bạn nắm vững kiến thức, bài viết dưới đây của Monkey sẽ trình bày chi tiết về công thức, phương pháp tính toán, cũng như mang đến một loạt bài tập ví dụ minh họa. Hãy cùng khám phá ngay!

Ôn tập lý thuyết hình thang cân

Trước khi đi sâu vào công thức tính diện tích hình thang cân, chúng ta hãy cùng ôn tập là một số lý thuyết về hình thang cân mà học sinh cần phải ghi nhớ.

Hình thang cân là gì?

Hình thang là gì? Hình thang là một khái niệm quen thuộc trong hình học phẳng. Cụ thể, hình thang là một tứ giác lồi trong đó có một cặp cạnh đối diện song song với nhau. Những cạnh này được gọi chung là "cạnh đáy" của hình thang. Trong khi đó, hai cạnh khác, không song song, được gọi là "cạnh bên". Các dạng đặc biệt của hình thang, bao gồm: Hình thang cân, hình thang vuông, hình thang vuông cân, hình bình hành,...

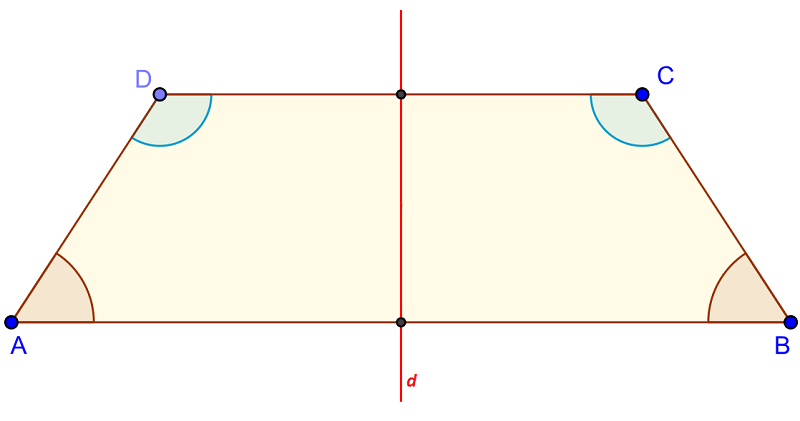
Hình thang cân là gì? Hình thang cân là một dạng đặc biệt của hình thang. Điểm nổi bật của nó chính là hai cạnh bên của hình thang này có độ dài bằng nhau. Điều này dẫn đến việc hai góc tạo bởi cạnh bên và một cạnh đáy sẽ có cùng kích thước.

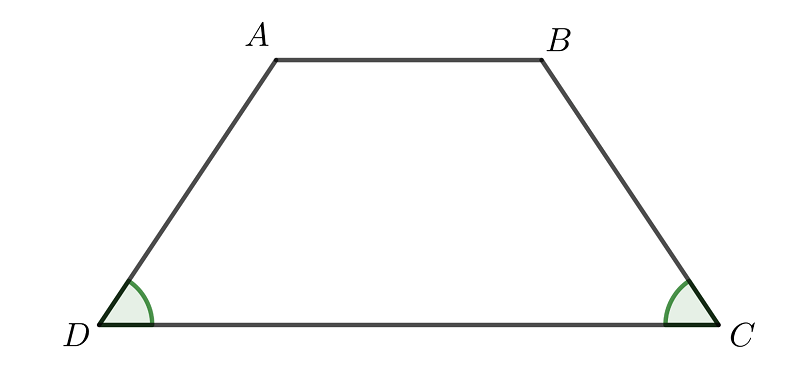
Tính chất của hình thang cân

Dưới đây là một số tính chất của hình thang cân mà bạn cần ghi nhớ:

Hai cạnh bên của hình thang cân bằng nhau.
Hai đường chéo của hình thang cân bằng nhau.
Trục đối xứng của hình thang cân bằng chiều cao của hình thang. Trong đó, trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm của hai cạnh đáy.

ĐỪNG BỎ LỠ!!

Chương trình học Toán bằng tiếng Anh, giúp phát triển tư duy một cách toàn diện nhất.

Nhận ưu đãi lên đến 40% NGAY TẠI ĐÂY!

Dấu hiệu nhận biết hình thang cân

Để nhận biết một hình thang cân trong các bài toán hình học hoặc thực tế, ta có thể dựa vào một số dấu hiệu đặc trưng, như sau:

Cạnh bên có độ dài bằng nhau: Trong hình thang cân, hai cạnh bên sẽ có độ dài giống nhau.
Đoạn nối giữa trung điểm hai cạnh bên (đường trung bình) song song với cả hai cạnh đáy.
Hình thang có hai góc kề một cạnh đáy bằng nhau, hay có một cặp góc đối xứng qua trung điểm của cạnh đáy, là hình thang cân.
Tính đối xứng: Nếu kẻ một đoạn thẳng vuông góc với cạnh đáy và đi qua trung điểm của cạnh đáy đó, bạn sẽ thấy hình thang cân được chia thành hai tam giác đồng dạng.

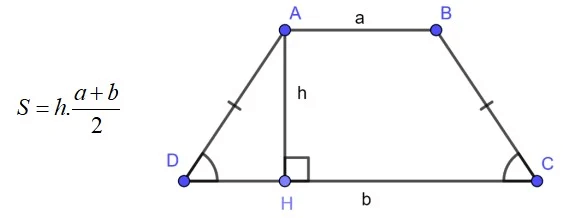
Công thức tính diện tích hình thang cân

Diện tích của hình thang cân được tính bằng tổng của hai cạnh đáy chia đôi, nhân với chiều cao.

Để tính diện tích của một hình thang cân, bạn có thể sử dụng công thức sau:

S = (a + b)/2 x h

Trong đó:

S là diện tích hình thang cân.
a và b là độ dài hai cạnh đáy.
h là chiều cao hình thang.

Ví dụ: Cho hình thang cân ABCD có đáy lớn AB = 10 cm, đáy nhỏ CD = 8 cm và chiều cao h = 6 cm. Diện tích hình thang cân ABCD là:

Giải:

Theo công thức tính diện tích hình thang cân, ta có:

S = (10 + 8)/2 x 6 = 54 cm2

Diện tích hình thang ABCD là 54 cm2.

Một số lưu ý khi tính diện tích hình thang cân:

Nếu chiều cao của hình thang cân không thể đo hoặc tính được trực tiếp thì ta có thể tính gián tiếp bằng cách sử dụng các tính chất của hình thang cân, như tính diện tích hình chữ nhật, diện tích tam giác,...
Diện tích hình thang cân luôn là một số dương.

Chu vi của hình thang cân được xác định bằng cách cộng độ dài hai cạnh đáy với tổng chiều dài của hai cạnh bên.

Để tính chu vi của một hình thang cân, bạn có thể sử dụng công thức sau:

P = a + b + (2 x c)

Trong đó:

P là chu vi hình thang cân.
a và b là độ dài hai cạnh đáy.
c là độ dài cạnh bên.

Ví dụ: Cho hình thang cân ABCD có đáy lớn AB = 15 cm, đáy bé CD = 10 cm và hai cạnh bên AD = BC = 7 cm. Tính chu vi hình thang ABCD.

Giải:

Theo công thức tính chu vi hình thang cân, ta có:

P = (2 x 7) + 15 + 10 = 39 cm

Chu vi hình thang ABCD là 39 cm.

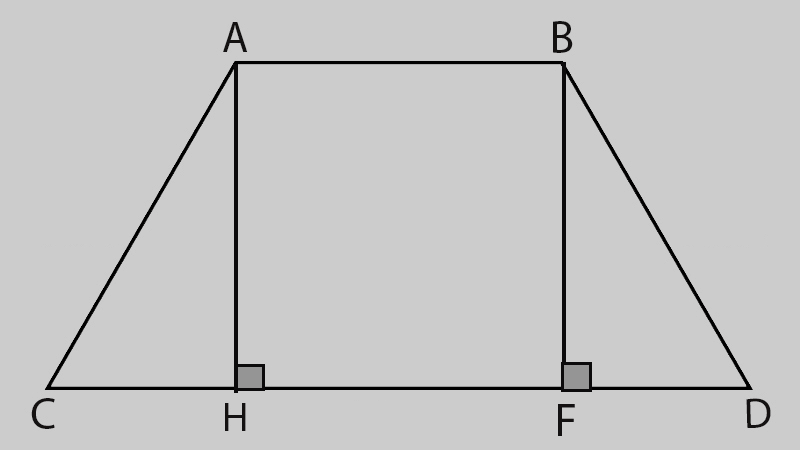
Lưu ý: Các công thức tính chu vi và diện tích hình thang cân cũng có thể áp dụng cho hình thang thường.

Các bài viết không thể bỏ lỡ

$\displaystyle$

Hình thang cân: Khái niệm, tính chất, dấu hiệu nhận biết & các công thức tính

$\displaystyle$

Chu vi hình thang cân: Công thức, cách tính và bài tập ví dụ

$\displaystyle$

Công thức tính chu vi hình thang vuông, bài tập và ứng dụng thực tiễn

Các bài tập ví dụ về phép tính diện tích hình thang cân

Bài 1: Cho hình thang cân EFGH có đáy lớn EF = 12 cm, đáy nhỏ GH = 6 cm và chiều cao h = 5 cm. Tính diện tích hình thang cân EFGH.

Giải:

Theo công thức tính diện tích hình thang cân, ta có:

S = (12 + 6)/2 x 5 = 45 cm2

Diện tích hình thang EFGH là 45 cm2.

Bài 2: Cho hình thang cân IJKL với IJ = 15 cm, KL = 5 cm, và h = 7 cm. Tính diện tích hình thang cân.

Giải:

Theo công thức tính diện tích hình thang cân, ta có:

S = (15 + 5)/2 x 7 = 70 cm2

Diện tích hình thang IJKL là 70 cm2.

Bài 3: Đáy lớn và đáy nhỏ của hình thang cân lần lượt là 20 cm và 10 cm, chiều cao là 8 cm. Hãy tính diện tích của nó.

Giải:

Theo công thức tính diện tích hình thang cân, ta có:

S = (20 + 10)/2 x 8 = 120 cm2

Diện tích hình thang là 120 cm2.

Bài 4: Hình thang cân có chiều cao 10 cm và hai đáy lần lượt là 7 cm và 13 cm. Tính diện tích của nó.

Giải:

Theo công thức tính diện tích hình thang cân, ta có:

S = (7 + 13)/2 x 10 = 100 cm2

Diện tích hình thang là 100 cm2.

Bài 5: Chiều cao của hình thang cân là 11 cm và hai đáy của nó lần lượt là 10 cm và 18 cm. Tính diện tích.

Giải:

Theo công thức tính diện tích hình thang cân, ta có:

S = (10 + 18)/2 x 11 = 154 cm2

Diện tích hình thang là 154 cm2.

Xem thêm:

Ứng dụng thực tiễn của diện tích hình thang cân

Diện tích hình thang cân có nhiều ứng dụng thực tế trong đời sống, chẳng hạn như:

Kiến trúc và xây dựng: Công thức tính diện tích hình thang cân được sử dụng để tính diện tích mặt bằng của các khu đất, sân vườn, hoặc các tầng trong các tòa nhà hình thang.

Ví dụ, khi tính diện tích mặt bằng của một ngôi nhà có hình dạng hình thang cân, ta có thể sử dụng công thức tính diện tích hình thang cân để tính diện tích của từng tầng, sau đó cộng diện tích của các tầng lại với nhau để có được diện tích mặt bằng tổng thể của ngôi nhà.

Thiết kế đồ trang sức: Công thức tính diện tích hình thang cân được sử dụng để tính diện tích của các viên đá quý hoặc viên kim cương có hình dạng hình thang trong việc tạo ra thiết kế độc đáo cho các món trang sức.

Ví dụ, khi thiết kế một chiếc nhẫn có viên đá quý hình thang cân, ta có thể sử dụng công thức tính diện tích hình thang cân để tính diện tích của viên đá quý, sau đó sử dụng diện tích này để tính kích thước của chiếc nhẫn.

Thiết kế nội thất: Công thức tính diện tích hình thang cân được sử dụng để tính diện tích của các đồ nội thất có dạng hình thang cân, chẳng hạn như bàn ghế, kệ sách, tủ quần áo,...

Ví dụ, khi thiết kế một chiếc bàn có mặt bàn hình thang cân, ta có thể sử dụng công thức tính diện tích hình thang cân để tính diện tích của mặt bàn, sau đó sử dụng diện tích này để tính kích thước của các chân bàn.

Ngoài ra, diện tích hình thang cân còn được sử dụng trong một số lĩnh vực như giáo dục, khoa học, kỹ thuật,...

Tóm lại, diện tích hình thang cân là một khái niệm toán học quan trọng có nhiều ứng dụng thực tiễn trong đời sống. Hy vọng rằng, những thông tin về hình thang cân mà Monkey cung cấp trên là hữu ích với bạn.