Danh sách các quy tắc toán học lớp 4 đầy đủ chi tiết nhất

Tổng hợp các quy tắc toán học lớp 4 đầy đủ nhất

Trong chương trình toán học lớp 4, các em sẽ phải ghi nhớ những quy tắc, công thức sau đây để hỗ trợ giải bài tập và học tốt kiến thức tốt hơn. Vậy nên, dưới đây Monkey sẽ tổng hợp các công thức liên quan để các em cùng nhau tìm hiểu:

Ôn tập về số tự nhiên

Một trong những phần kiến thức mà bé sẽ được học trong chương trình toán lớp 4 đầu tiên chính là về số tự nhiên. Đây là nội dung cơ bản để hỗ trợ trẻ có thể tính toán và học tập hiệu quả. Một số nội dung trọng tâm của số tự nhiên như sau:

* Số và chữ số

Số tự nhiên chính là các chữ số được thành lập từ 10 chữ số cơ bản từ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Tính chất của những số tự nhiên này như sau:

• Có tổng cộng 10 số có 1 chữ số (0 – 9)

• Có tổng cộng 90 số có hai chữ số (10 - 99)

• Có tổng cộng 900 số có ba chữ số (100 - 999)

• Có tổng cộng 9000 số có bốn chữ số (1000 - 9999)

• Số tự nhiên nhỏ nhất là 0 và không có số tự nhiên lớn nhất.

• Các số tự nhiên liên tiếp nhau sẽ hơn hoặc kém nhau một đơn vị.

• Số chẵn trong dãy số tự nhiên sẽ có tận cùng là các số 0, 2, 4, 6, 8. Trong đó, hai số chẵn gọi là liên tiếp nhau sẽ hơn hoặc kém nhau 2 đơn vị.

• Số lẻ là những chữ số tự nhiên có tận cùng là 3, 5, 7, 9. Hai số lẻ gọi là liên tiếp nhau sẽ hơn hoặc kém nhau 2 đơn vị.

* Hàng và lớp

Hàng và lớp toán lớp 4 chính là kiến thức trọng tâm để hỗ trợ bé xác định được giá trị của số tự nhiên chính xác. Cụ thể:

• Hàng đơn trăm, hàng chục, hàng đơn vị sẽ tạo thành lớp đơn vị

• Hàng trăm nghìn, hàng chục nghìn, hàng nghìn sẽ tạo thành lớp nghìn.

• Để hiểu đơn giản hơn, mọi người có thể tham khảo bảng hàng và lớp sau:

• Để giải được bài tập hàng và lớp toán lớp 4, các em cần chú ý những vấn đề sau:

• Cách đọc: Các em sẽ đọc số tự nhiên theo thứ tự từ trái qua phải hoặc từ cao đến thấp.

• Các chữ số từ phải qua trái lần lượt sẽ là các hàng đơn vị, hàng chục, hàng trăm, hàng nghìn, hàng chục nghìn, hàng trăm nghìn…

Dãy số

Dựa theo số tự nhiên, các dãy số sẽ được sắp xếp theo thứ tự từ nhỏ đến lớn như sau: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10;…

Một số quy tắc của một dãy số tự nhiên toán lớp 4 mà bé cần nắm rõ:

• Nếu dãy số liên tiếp bắt đầu chỗ chẵn, kết thúc số lẻ và ngược lại thì số lượng số chẵn sẽ bằng số lẻ.

• Nếu một dãy số liên tiếp bắt đầu là số chẵn, kết thúc số chẵn thì số lượng số chẵn nhiều hơn số lượng số lẻ là 1.

• Nếu một dãy số liên tiếp bắt đầu là số lẻ, kết thúc số lẻ thì số lượng số lẻ nhiều hơn số lượng số chẵn là 1.

Trong phần dãy số có thêm thuật ngữ “dãy số cách đều”. Nên để tính được các số hạng của dãy số này ta có công thức: 

Số số hạng = (số hạng cuối – số hạng đầu) : d + 1

Tổng = [ (số đầu + số cuối) x số số hạng] : 2

Ví dụ 1: Tính số số hạng của dãy số 2, 4, 6, 8… 10, 12.

Hướng dẫn giải:

Ta có 4 – 2 = 2; 6 – 4 = 2. Nên đây được xem là dãy số cách đều.

Suy ra ta có số số hạng của dãy cách đều trên: (12 – 2) : 2 +1 = 6

Ví dụ 2: Tính tổng của dãy số: 2, 4, 6, 8… 10, 12.

Tổng của dãy số cách đều trên =  [(12 + 2) x 6] : 2 = 42.

Phép cộng

Phép cộng là phép tính cơ bản trong toán học, dùng để tính tổng các đại lượng hay số hàng với nhau.

Ký hiệu:  “+”.

Ta có: a + b = c

Trong đó: a và b là các số hạng trong tổng, c là tổng của phép toán cộng.

Một số tính chất của phép cộng các bé cần nắm rõ:

• Tính chất giao hoàn: Trong phép tính cộng, khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi. → a + b = b + a

• Tính chất kết hợp: Trong một phép tính cộng, khi cộng tổng hai số với một số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba. → (a + b) + c = a + (b + c)

• Tính chất cộng với 0: Bất cứ số nào cộng với 0 thì cũng bằng chính nó. → a + 0 = 0 + a = a

• Trong một tổng có các số hạng lẻ là một số lẻ thì tổng đó là một số lẻ.

• Trong một tổng có các số hạng lẻ là chẵn thì tổng đó là một số chẵn.

• Tổng của các số hạng chẵn là một số chẵn.

• Tổng của một số hạng lẻ và một số hạng chẵn là một số lẻ.

• Tổng của hai số tự nhiên liên tiếp là một số hạng lẻ.

Phép trừ

Phép trừ là phép tính giảm bớt số phần từ từ một con số nào đó để có được kết quả chính xác.

Ký hiệu: “-”.

Ta có: a – b = c

Trong đó, ta có a là số bị trừ, b là số trừ, c là hiệu của phép trừ.

Để thực hiện được phép tính trừ các số tự nhiên, ta cần nắm rõ các điều kiện sau:

• Số bị trừ trong phép tính phải luôn luôn lớn hơn hoặc bằng số trừ.

• Thực hiện phép trừ theo thứ tự từ trái sang phải.

Một số tính chất trong phép trừ:

• Trừ đi số 0: Bất kỳ một số tự nhiên nào trừ đi 0 thì vẫn bằng chính nó. → a – 0 = a

• Trừ đi chính nó: Bất kỳ một số tự nhiên nào khi trừ đi chính nó thì sẽ bằng 0. → a – a = 0

• Trừ đi một tổng: Khi thực hiện phép trừ của một số tự nhiên cho một tổng, ta có thể lấy số đó trừ cho từng số hạng của tổng đó. → a – (b + c) = a – b – c = a – c – b.

• Trừ đi một hiệu: Khi thực hiện phép trừ của một số tự nhiên cho một hiệu, ta có thể lấy số đó trừ cho số bị trừ rồi cộng với số trừ. →  a – (b – c) = a – b + c = a + c – b.

• Trong một phép trừ, nếu số bị trừ và số trừ cùng tăng (hoặc cùng giảm) n đơn vị thì hiệu của chúng không đổi.

• Trong một phép trừ, nếu số bị trừ được gấp lên n lần và giữ nguyên số trừ thì hiệu được tăng thêm một số đúng bằng (n – 1) lần số bị trừ (n > 1).

• Trong một phép trừ, nếu số bị trừ giữ nguyên, số trừ được gấp lên n lần thì hiệu bị giảm đi (n – 1) lần số trừ  (n > 1).

• Trong một phép trừ, nếu số bị trừ được tăng thêm n đơn vị, số trừ giữ nguyên thì hiệu tăng lên n đơn vị.

• Trong một phép trừ, nếu số bị trừ tăng lên n đơn vị, số trừ giữ nguyên thì hiệu giảm đi n đơn vị.

Các quy tắc toán học lớp 4 về phép nhân

Phép nhân cũng là một trọng 4 phép tính cơ bản trong toán học, cùng để tìm hai hay nhiều số tự nhiên thông qua việc cộng lặp lại các số đó.

Ký hiệu: Dấu “x” hoặc dấu “.”.

Ta có: a x b = c

Trong đó: a, b gọi là các thừa số và c là tích của các thừa số.

Một số tính chất của phép tính nhân:

• Tính chất giao hoán: Khi hoàn đổi vị trí các thừa số trong một tích thì tích sẽ không thay đổi. → a x b = b x a

• Tính chất kết hợp: Khi thực hiện phép nhân hai số tự nhiên với số thứ ba, ta có thể nhân số thứ nhất với tích hai số còn lại. → (a x b) x c = a x (b x c)

• Tính chất nhân với số 0: Bất kỳ số tự nhiên nào nhân với số 0 thì tích sẽ bằng 0. → a x 0 = 0 x a = 0

• Tính chất nhân với số 1: Bất kỳ số tự nhiên nào khi nhân với 1 thì cũng bằng chính nó. → a x 1 = 1 x a = a

• Nhân một số với một tổng: Khi nhân một số tự nhiên với một tổng, ta có thể lấy số đó nhân với từng số hạng của tổng và cộng các kết quả với nhau. → a x (b + c) = a x b + a x c 

• Nhân một số với một hiệu: Khi nhân một số tự nhiên với một hiệu, ta có thể lấy số đó nhân với số bị trừ và số trừ rồi trừ hai kết quả đó với nhau. → a x (b – c) = a x b – a x c

• Trong một tích nếu một thừa số được gấp lên n lần đồng thời có một thừa số khác bị giảm đi n lần thì tích của phép nhân đó sẽ không thay đổi.

• Trong một tích có một thừa số được gấp lên n lần, các thừa số còn lại giữ nguyên giá trị thì tích được gấp lên n lần và ngược lại nếu trong một tích có một thừa số bị giảm đi n lần, các thừa số còn lại giữ nguyên thì tích đó cũng bị giảm đi n lần. (n > 0)

• Trong một tích, nếu một thừa số được gấp lên n lần, đồng thời một thừa số khác cũng được gấp lên m lần thì tích được gấp lên (m × n) lần. Ngược lại nếu trong một tích có một thừa số bị giảm đi m lần, một thừa số khác cũng bị giảm đi n lần thì tích đó bị giảm đi (m × n) lần (m và n khác 0).

• Trong một tích, nếu một thừa số được tăng thêm a đơn vị, các thừa số còn lại giữ nguyên thì tích được tăng thêm a lần tích các thừa số còn lại của phép nhân.

• Trong một tích, nếu có ít nhất một thừa số là số chẵn thì tích đó là số chẵn.

• Trong một tích, nếu có ít nhất một thừa số là số tròn chục hoặc ít nhất một thừa số có chữ số tận cùng là 5 và có ít nhất một thừa số chẵn thì tích sẽ có chữ số tận cùng là 0.

• Trong một tích các thừa số đều lẻ và có ít nhất một thừa số có chữ số tận cùng là 5 thì tích có tận cùng là 5.

Phép chia

Phép chia chính là phép tính ngược của phép nhân. Nên khi chia các số tự nhiên, kết quả sẽ được gọi là thương và sẽ có hai trường hợp đó là phép chia hết và phép chia có dư.

Ký hiệu: Dấu “:” hoặc “/”.

Ta có: a : b = c

Trong đó, ta có a là số bị chia, b là số chia và c là thương của phép chia.

Lưu ý: Số chia b luôn luôn khác 0 thì phép chia mới có nghĩa.

Một số tính chất của phép chia các em cần ghi nhớ:

Chia một số cho 1: Bất kỳ một số tự nhiên nào khi chia cho 1 thì vẫn bằng chính nó.

→ a : 1 = a 

Chia một số cho chính nó: Bất kỳ số tự nhiên nào khi chia cho chính nó thì sẽ bằng 1.

→ a : a = 1

Số 0 chia cho một số tự nhiên: Khi số 0 chia cho một số tự nhiên khác 0 thì kết quả sẽ bằng 0.

→ 0 : a = 0

Một tổng chia cho một số tự nhiên: Khi thực hiện phép chia một tổng cho một số tự nhiên khác 0, ta lấy từng số hạng của tổng đó chia cho số chia và cộng các kết quả lại với nhau. (Trong trường hợp các số hạng đó đều chia hết cho số chia).

→ (a + b) : c = a : c + b : c

Một hiệu chia cho một số tự nhiên: Khi thực hiện phép chia một trừ cho một số tự nhiên khác 0, ta lấy từng số bị trừ và số trừ của hiệu đó chia cho số chia và trừ các kết quả lại với nhau. (Trong trường hợp số bị trừ và số trừ đó đều chia hết cho số chia).

→ (a – b) : c = a : c – b : c

Chia một số cho một tích: Khi chia một số tự nhiên cho một tích, ta có thể chia số đó cho một thừa số, rồi lấy kết quả vừa tìm chia tiếp cho thừa số kia.

→ a : (b x c) = a : b : c = a : c : b

Chia một tích cho một số tự nhiên: Khi chia một tích cho một số tự nhiên, ta có thể lấy một thừa số chia cho số chia (trường hợp chia hết), rồi lấy kết quả vừa tìm nhân với thừa số kia.

→ (a x b) : c = a : c x b = b : c x a

Tính chất chia hết của dãy số tự nhiên

Bên cạnh việc thành thạo các phép tính, các em cần phải nắm rõ dấu hiệu phép chia hết cho các số 2, 3, 5, 9 để tính toán nhanh hơn. Cụ thể:

Các số tự nhiên có chữ số tận cùng là 0, 2, 4, 6, 8 thì số đó chia hết cho 2.

Ví dụ: Các số 2, 24, 48, 66,… đều chia hết cho 2 vì chúng đều là số có tận cùng là các số 2, 4, 6, 8.

Các số tự nhiên có tổng các chữ số chia hết cho 3 thì số đó sẽ chia hết cho 3.

Ví dụ: 252 chia hết cho 3 vì trong số 252 có tổng các chữ số 2 + 5 + 2 = 9 chia hết cho 3.

Các số tự nhiên có chữ số tận cùng là 0 hoặc 5 thì số đó chia hết cho 5.

Ví dụ: 205, 2005, 4000 chia hết cho 5 vì các số trên đều có chữ số tận cùng là 0 và 5.

Các số tự nhiên có tổng các chữ số chia hết cho 9 thì số đó chia hết cho 9.

Ví dụ: 8766 chia hết cho 9 vì trong số 657 có tổng các chữ số 8 + 7 + 6 + 6= 21 chia hết cho 9.

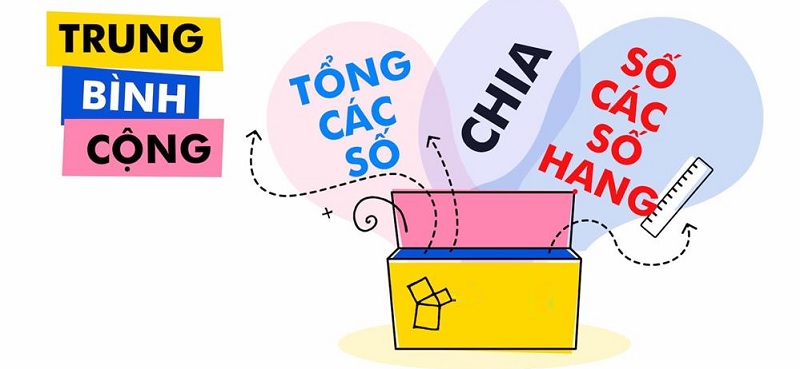
Toán Trung bình cộng

Để tìm được trung bình cộng (TBC) của dãy số tự nhiên, ta sẽ tính tổng của chúng rồi chia cho các số hạng. Cụ thể:

TBC = tổng các số hạng : số các số hạng

Ngược lại, để tìm tổng các số tự nhiên, ta lấy TBC nhân với số các số hạng.

Ví dụ: Tìm số trung bình cộng của các số sau: 3, 5, 7, 9, 11, 13, 15

→ TBC = (3 + 5 + 7 + 9 + 11 + 13 + 15) : 7 = 9

XÂY DỰNG NỀN TẢNG TOÁN HỌC, PHÁT TRIỂN TƯ DUY NĂNG LỰC HỌC TOÁN VÀ PHÁT TRIỂN NGÔN NGỮ CHO TRẺ CÙNG VỚI MONKEY MATH CHỈ VỚI 2K/NGÀY.

Các quy tắc toán học lớp 4 về toán tỉ lệ thuận

Trong toán học, hai đại lượng tỉ lệ thuận chính là khi một đại lượng tăng hoặc giảm bao nhiêu lần thì đại lượng còn lại cũng sẽ tăng hoặc giảm từng đó lần.

Ví dụ: Một ô tô trong hai giờ đi được 90km. Hỏi trong 4 giờ ô tô đó đi được bao nhiêu ki- lô- mét?

Tóm tắt:

2 giờ: 90 km

4 giờ: … km?

Bài giải

Cách 1:

Trong một giờ ô tô đi được là:

90 : 2 = 45 (km) (*)

Trong 4 giờ ô tô đi được là:

45 × 4 = 180 (km)

Đáp số: 180 km

Cách 2:

4 giờ gấp 2 giờ số lần là:

4 : 2 = 2 (lần) (**)

Trong 4 giờ ô tô đi được là:

90 × 2 = 180 (km)

Đáp số: 180 km

Toán tỉ lệ nghịch

Ngược lại với toán tỉ lệ thuận, nếu hai đại lượng tỉ lệ nghịch là khi một đại lượng tăng hoặc giảm bao nhiêu lần thì đại lượng còn lại sẽ giảm hoặc tăng từng đó lần.

Ví dụ: Muốn đắp xong nền nhà trong hai ngày, cần có 12 người. Hỏi muốn đắp xong nền nhà đó trong 4 ngày thì cần có bao nhiêu người? (Mức làm của mỗi người như nhau)

Tóm tắt:

2 ngày: 12 người

4 ngày: …. người?

Bài giải

Cách 1:

Muốn đắp xong nền nhà trong 1 ngày, cần số người là:

12 × 2 = 24 (người) (*)

Muốn đắp xong nền nhà trong 4 ngày, cần số người là:

24 : 4 = 6 (người)

Đáp số: 6 người

Cách 2:

4 ngày gấp 2 ngày số lần là:

4 : 2 = 2 (lần)

Muốn đắp xong nền nhà trong 4 ngày, cần số người là:

12 : 2 = 6 (người)

Đáp số: 6 người

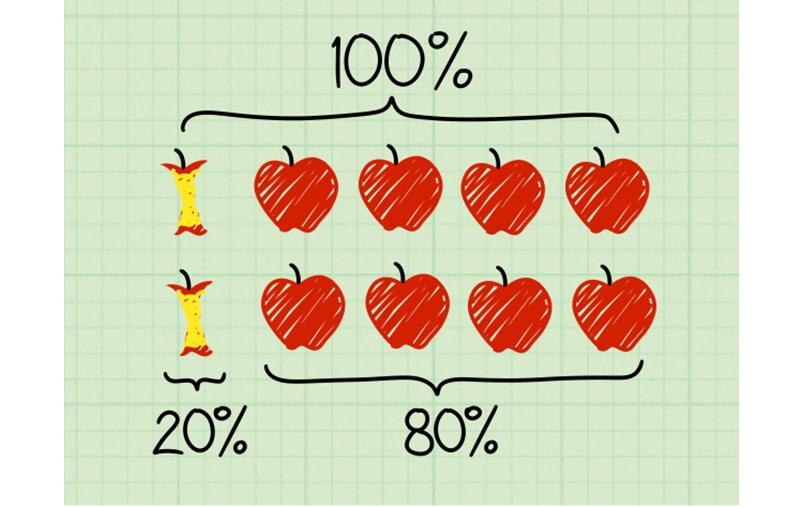
Tỉ số phần trăm

Tỉ số phần trăm là phần kiến thức không chỉ ứng dụng trong toán học lớp 4 mà còn cả thực tiễn. Ký hiệu %.

Quy tắc 1: Để tìm được tỉ số phần trăm của hai số thì các em cần phải làm theo các bước như sau:

• Bước 1: Tìm thương của hai số đó dưới dạng số thập phân.

• Bước 2: Nhân thương đó với 100 và viết thêm kí hiệu phần trăm (%) vào bên phải tích tìm được.

Công thức: a : b = T (STP) = STP × 100 (%)

Ví dụ: Tìm tỉ số phần trăm của 315 và 600

Giải

Tỉ số phần trăm của 315 và 600 là:

315 : 600 = 0,525 = 52,5 %

Đáp số: 52,5 %

Quy tắc 2: Để tìm giá trị % của số cho trước, ta chỉ cần lấy giá trị đó chia cho 100 rồi nhân số % hoặc lấy số đó nhân với số % rồi chia cho 100.

Công thức: Giá trị % = Số A : 100 × số % hoặc Giá trị % = Số A × số % : 100

Ví dụ: Trường Đại Từ có 600 học sinh. Số học sinh nữ chiếm 45% số học sinh toàn trường. Tính số học sinh nữ của trường.

Giải

Số học sinh của trường đó là:

600 : 100 × 45 = 270 (học sinh)

Đáp số: 270 học sinh

Quy tắc 3: Để tìm một số thông qua giá trị phần trăm của chúng, ta chỉ cần lấy giá trị đó chia cho số phần trăm nhân với 100, hoặc lấy giá trị % nhân 100 rồi chia cho số %.

Công thức: Số A = Giá trị % : số phần trăm × 100 hoặc Số A = Giá trị % × 100 : số phần trăm

Ví dụ: Tìm một số biết 30% của nó bằng 72.

Giải

Giá trị của số đó là:

72 : 30 × 100 = 240

Đáp số: 240

Các quy tắc toán học lớp 4 về đại lượng

Các đại lượng trong toán học khá nhiều, nhưng tính ứng dụng trong thực tiễn rất cao. Nên đòi hỏi các em phải nắm vững để giải bài tập hay ứng dụng tốt nhất. Cụ thể:

* Bảng đơn vị đo độ dài

Theo đó:

• Mỗi đơn vị đo độ dài đều gấp 10 lần đơn vị bé hơn liền sau nó.

• Mỗi đơn vị đo độ dài đều kém hơn 10 lần đơn vị lớn hơn liền trước nó.

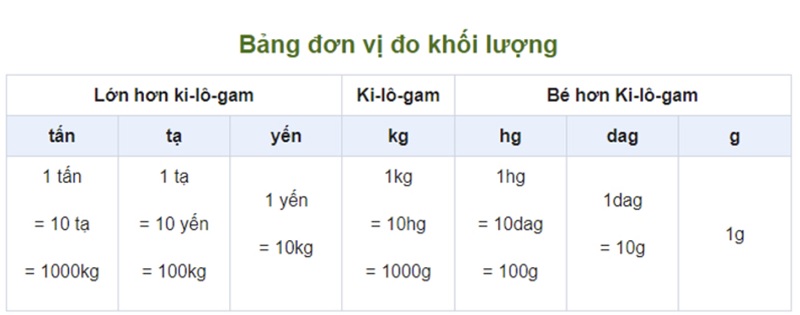
* Bảng đơn vị đo khối lượng

Dưới đây là bảng đơn vị đo khối lượng chi tiết nhất:

• Để đo các đồ vật hàng hàng chục, trăm, ngàn ki lô gam ta sẽ dùng đơn vị yến tạ tấn.

• Để đo các đồ vật nặng từ hàng chục, trăm, ngàn gam ta dùng đề-ca-gam, héc-tô-gam.

• Mỗi đơn vị đo khối lượng đều gấp 10 lần đơn vị bé hơn liền sau nó.

• Mỗi đơn vị đo khối lượng đều kém hơn 10 lần đơn lớn hơn liền trước nó.

* Bảng đơn vị đo diện tích

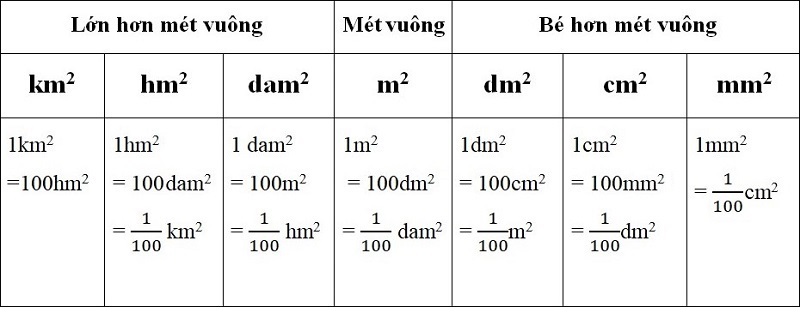
Lưu ý: Trong bảng đơn vị đo diện tích, hai đơn vị đo diện tích liền nhau gấp (hoặc kém) nhau 100 lần.

* Bảng đơn vị đo thể tích

Trong đó: Trong bảng đơn vị đo thể tích, hai đơn vị đo thể tích liền nhau gấp (hoặc kém) nhau 1000 lần.

Lưu ý: 1dm3 = 1 l

* Các quy tắc toán học lớp 4 về Giây – thế kỷ

Giây – thế kỷ toán lớp 4 là đơn vị đo thời gian, giúp các em luyện tập kỹ năng xem giờ giấc, tính toán thời gian một cách chính xác.

Trong đó:

• 1 thế kỷ = 100 năm

• Từ năm 1 đến năm 100 là thế kỷ 1 (thế kỷ I).

• Từ năm 101 đến năm 200 là thế kỷ 2 (thế kỷ II).

• Từ năm 201 đến năm 300 là thế kỷ 3 (thế kỷ III).

• 1 năm = 365 ngày

• 1 năm nhuận = 366 ngày

• Một năm có 12 tháng.

• Tháng 1, 3, 5, 7, 8, 10, 12: có 31 ngày.

• Tháng 4, 6, 9, 11: có 30 ngày.

• Tháng hai có 28 ngày (năm nhuận có 29 ngày)

• 1 phút = 60 giây

• 1 giờ = 60 phút = 3600 giây

Ôn tập hình học

Bên cạnh đại số, hình học toán lớp 4 cũng sẽ bao gồm nhiều kiến thức, quy tắc quan trọng mà các em cần phải nắm rõ để chinh phục bài tập và ứng dụng trong thực tiễn. Cụ thể:

* Hình vuông

Hình vuông là tứ giác có 4 góc vuông, 4 cạnh dài bằng nhau.

Công thức tính chu vi hình vuông: Muốn tính chu vi hình vuông, ta lấy số đo một cạnh nhân với 4.

→ P = a x 4

Trong đó: a là cạnh và P là chu vi.

Muốn tìm một cạnh hình vuông, ta lấy chu vi chia cho 4.

→ a = P : 4

Công thức tính diện tích hình vuông: Ta lấy số đo một cạnh nhân với chính nó.

→ S = a x a

Để tìm 1 cạnh hình vuông khi biết diện tích, ta tìm xem một số nào đó nhân với chính nó bằng diện tích, thì đó là cạnh.

* Hình chữ nhật

Hình chữ nhật là tứ giác có 4 góc vuông, 2 chiều dài bằng nhau, 2 chiều rộng bằng nhau.

Công thức tính chu vi: Ta lấy số đo chiều dài cộng số đo chiều rộng(cùng đơn vị đo) rồi nhân với 2.

→ P = (a + b) × 2

Trong đó: chiều dài là a, chiều rộng là b và P là chu vi.

Để tìm chiều dài, ta lấy chu vi chia cho 2 rồi trừ đi chiều rộng. a = P : 2 - b

Để tìm chiều rộng, ta lấy chu vi chia cho 2 rồi trừ đi chiều dài. b = P : 2 - a

Công thức tính diện tích: ta lấy số đo chiều dài nhân với số đo chiều rộng (cùng đơn vị đo).

→ S = a × b

Để tìm chiều dài, ta lấy diện tích chia cho chiều rộng. a = S : b

Để tìm chiều rộng, ta lấy diện tích chia cho chiều dài. b = S : a

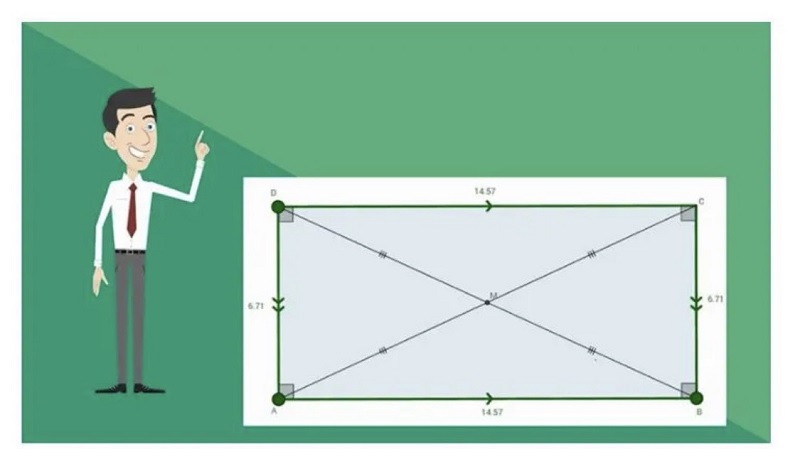
* Hình bình hành

Hình bình hành có hai cặp cạnh đối diện song song và bằng nhau.

Công thức tính chu vi hình bình hành: Ta tính bằng tổng độ dài của 4 cạnh hoặc bằng tổng hai cạnh đáy nhân với 2.

→ P = (a + b) x 2

Công thức tính diện tích hình bình hành: ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo)

→ S = a × h

Để tìm độ dài đáy, ta lấy diện tích chia cho chiều cao. a = S : b

Để tìm chiều rộng, ta lấy diện tích chia cho chiều dài. b = S : a

Trong đó: Đáy là a, chiều cao là h

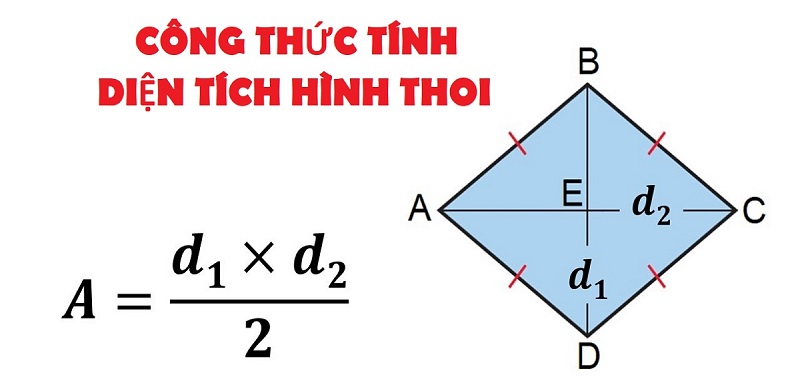
* Hình thoi

Tính chất:

• Hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau

• Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

Công thức tính chu vi hình thoi: Ta lấy số đo một cạnh nhân với 4.

→ P = a x 4

Công thức tính diện tích hình thoi: Ta lấy tích của độ dài hai đường chéo chia cho 2 (cùng đơn vị đo). 

→ S = ½ x (m x n ) hoặc S = h x a

Trong đó:

• a: Cạnh hình thoi

• h: Chiều cao hình thoi

• m, n: Hai đường chéo

• P: Chu vi

• S: Diện tích

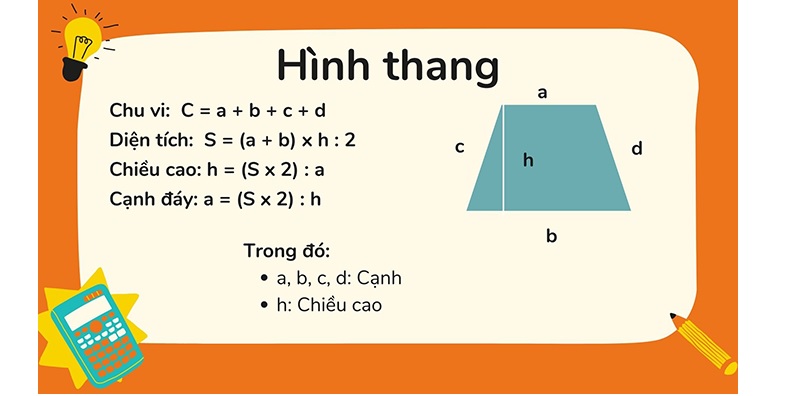
* Hình thang

Hình thang có một cặp cạnh đối diện song song. Trong đó chiều cao chính là đoạn thẳng ở giữa hai đáy và vuông góc với hai đáy.

Công thức tính diện tích hình thang: Ta lấy tổng độ dài hai đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho 2.

→ S = (a + b) x h : 2

Để tính tổng hai đáy hình thoi ta lấy diện tích nhân với 2 rồi chia cho chiều cao.

→ (a + b) = S x 2 : h

Để tính trung bình cộng hai đáy ta lấy diện tích chia cho chiều cao. 

→ a hoặc b= S : h

Để tính độ dài đáy lớn hình thang: Ta lấy diện tích nhân với 2, chia cho chiều cao rồi trừ đi độ dài đáy bé. 

→ a = S x 2 : h - b

Để tính độ dài đáy bé hình thang: Ta lấy diện tích nhân với 2, chia cho chiều cao rồi trừ đi độ dài đáy lớn.

→ b = S x 2 : h - a

Để tính chiều cao hình thang: Ta lấy diện tích nhân với 2 rồi chia cho tổng độ dài hai đáy.

→ h = S x 2 : (a + b)

hoặc: Tính chiều cao: Ta lấy diện tích chia cho trung bình cộng của hai đáy.

Trong đó: đáy lớn là a, đáy nhỏ là b, chiều cao là h

* Hình tam giác

Hình tam giác có ba cạnh, 3 góc, 3 đỉnh. Chiều cao hình tam giác chính là đoạn thẳng hạ từ đỉnh vuông góc với cạnh đối diện.

Công thức tính chu vi hình tam giác: Bằng tổng độ dài của 3 cạnh.

→ P = a + b + c

Công thức tính diện tích hình tam giác: Ta lấy độ dài đáy nhân với chiều cao (cùng đơn vị đo) rồi chia cho 2.

→ S = a x h : 2

Để tính cạnh đáy hình tam giác: Ta lấy diện tích nhân với 2 rồi chia cho chiều cao.

→ a = S x 2 : h

Để tính chiều cao hình tam giác: Ta lấy diện tích nhân với 2 rồi chia cho cạnh đáy.

→ h = S x 2 : a

* Hình tròn

• Hình tròn có tất cả các bán kính bằng nhau.

• Đường bao quanh hình tròn gọi là đường tròn.

• Điểm chính giữa hình tròn là tâm.

• Đoạn thẳng nối tâm với một điểm trên đường tròn gọi là bán kính. Ki hiệu là r

• Đoạn thẳng đi qua tâm và nối hai điểm của đường tròn gọi là đường kính.

• Đường kính gấp hai lần bán kính. Kí hiệu là d

Công thức tính chu vi hình tròn: Ta lấy đường kính nhân với số 3,14.

→ C = d x 3,14

Hoặc ta lấy bán kính nhân 2 rồi nhân với số 3,14.

→ C = r x 2 x 3,14

Để tính đường kính hình tròn: Ta lấy chu vi chia cho số 3,14

→ d = C : 3,14

Để tính bán kính hình tròn: ta lấy chu vi chia cho 2 rồi chia cho số 3,14

→ r = C : 2 : 3,14 (Tính ra nháp: r = C : 6,28)

Công thức tính diện tích hình tròn: Ta lấy bán kính nhân với bán kính rồi nhân với số 3,14. 

→ S = r x r x 3,14

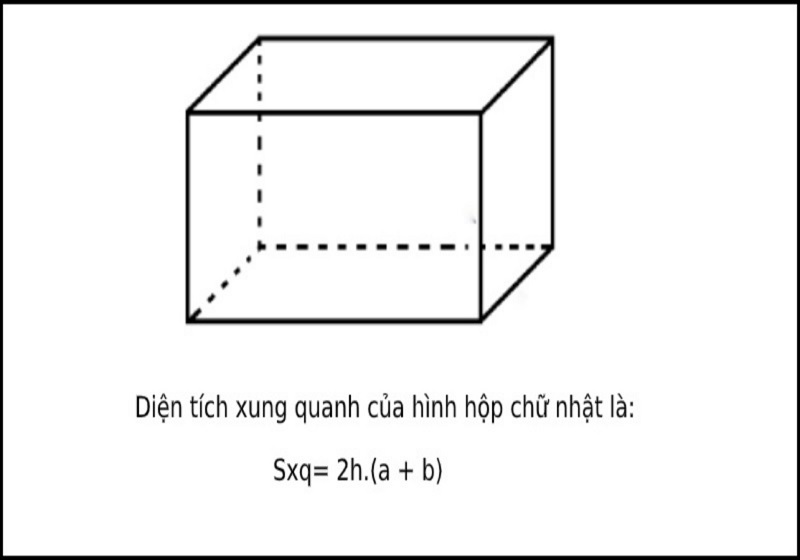
* Hình hộp chữ nhật

• Hình hộp chữ nhật có 6 mặt, hai mặt đáy và bốn mặt bên.

• Có 8 đỉnh, 12 cạnh

• Có ba kích thước: chiều dài (a), chiều rộng (b), chiều cao (c).

Công thức tính diện tích xung quanh hình hộp chữ nhật: Ta lấy chu vi đáy nhân với chiều cao (cùng một đơn vị đo).

→ S(xung quanh) = P(đáy) x c Hoặc: S(xung quanh) = (a + b) x 2 x c

Để tìm chu vi đáy, ta lấy diện tích xung quanh chia cho chiều cao.

→ P (đáy) = S(xung quanh) : c

Để tìm chiều cao hình hộp chữ nhật, ta lấy diện tích xung quanh chia cho chu vi đáy

→ c = S(xung quanh) : P (đáy)

Để tìm tổng hai đáy hình hộp chữ nhật, ta lấy diện tích xung quanh chia cho 2 rồi chia cho chiều cao.

→ (a + b) = S(xq) : 2 : h

Để tìm chiều dài hình hộp chữ nhật, ta lấy diện tích xung quanh chia cho 2, chia cho chiều cao rồi trừ đi chiều rộng.

→ a = S(xq) : 2 : c - b

Để tìm chiều rộng hình hộp chữ nhật, ta lấy diện tích xung quanh chia cho 2, chia cho chiều cao rồi trừ đi chiều dài.

→ b = S(xq) : 2 : c - a

Để tính diện tích toàn phần hình hộp chữ nhật: Ta lấy diện tích xung quanh cộng diện tích hai đáy.

→ Stp = S(xq) + S (2đáy) Hoặc: Stp = (a + b ) x 2 x c + a x b x 2

Để tìm diện tích đáy hình hộp chữ nhật ta lấy chiều dài nhân với chiều rộng.

→ S(đáy) = a x b

Để tìm chiều dài hình hộp chữ nhật, ta lấy diện tích đáy chia cho chiều rộng.

→ a = S(đáy) : b

Để tìm chiều rộng hình hộp chữ nhật, ta lấy diện tích đáy chia cho chiều dài.

→ b = S (đáy) : a

Công thức tính thể tích hình hộp chữ nhật: ta lấy chiều dài nhân với chiều rộng rồi nhân với chiều cao (cùng một đơn vị đo).

→ V = a x b x c

Để tìm chiều dài hình hộp chữ nhật, ta lấy thể tích chia cho chiều rộng rồi chia tiếp cho chiều cao.

→ a = V : b : c

Để tìm chiều rộng, ta lấy thể tích chia cho chiều dài rồi chia tiếp cho chiều cao.

→ b = V : a : c

Để tìm chiều cao, ta lấy thể tích chia cho chiều dài rồi chia tiếp cho chiều rộng.

→ c = V : a : b

hoặc lấy thể tích chia cho diện tích đáy

→ c = V : S(đáy)

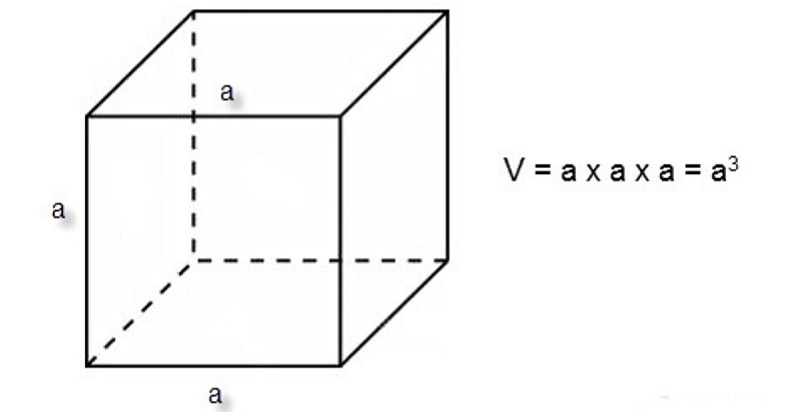
* Hình lập phương

• Hình lập phương có 6 mặt là các hình vuông bằng nhau.

• Có 8 đỉnh, 12 cạnh dài bằng nhau. Kí hiệu cạnh là a

Công thức tính diện tích xung quanh hình lập phương: Ta lấy diện tích một mặt nhân với 4

→ S×q = S(1 mặt) × 4

Để tính diện tích toàn phần hình lập phương: Ta lấy diện tích một mặt nhân với 6

→ Stp = S(1 mặt) × 6

Để tính diện tích một mặt ta lấy diện tích xung quanh chia cho 4 hoặc diện tích toàn phần chia cho 6.

→ S(1 mặt) = S×q : 4 hoặc S(1 mặt) = Stp : 6

Để tính 1 cạnh hình lập phương, ta tìm xem một số nào đó nhân với chính nó bằng diện tích một mặt, thì đó là cạnh.

Công thức tính thể tích hình lập phương: Ta lấy cạnh nhân với cạnh rồi nhân với cạnh.

→ V = a × a × a

Để tính 1 cạnh hình lập phương, ta tìm xem một số nào đó nhân với chính nó rồi nhân tiếp với nó bằng thể tích, thì đó là cạnh.

Chỉ với khoảng 10 phút học tiếng Anh mỗi ngày cùng Monkey Junior, con có thể tích lũy 1.000 từ vựng tiếng Anh/ năm.

Các quy tắc toán học lớp 4 về phân số và các phép tính phân số

Phân số cũng là phần kiến thức quan trọng trong chương trình toán lớp 4, nếu không nắm rõ các quy tắc bé sẽ khó chinh phục được dạng toán này.

* Khái niệm phân số

Phân số là số được cấu tạo gồm tử số và mẫu số. Trong đó, tử số chính là số tự nhiên nằm trên dấu gạch. Mẫu số là số tự nhiên khác 0 viết dưới dấu gạch.

Một số tính chất cơ bản của phân số:

• Tất cả số tự nhiên để có thể viết được dưới dạng phân số có tử số là số tự nhiên đó và mẫu số bằng 1.

• Số 1 có thể viết thành dạng phân số có tử số và mẫu số bằng nhau và khác 1.

• Số 0 có thể viết thành dạng phân số có tử số là 0 và mẫu số khác 0.

• Nếu nhân cả tử số và mẫu số của một phân số bất kỳ với cùng một số tự nhiên khác 0 thì ta được một phân số mới bằng phân số đã cho.

• Nếu chia cả tử số và mẫu số của một phân số bất kỳ với cùng một số tự nhiên khác 0 thì ta được một phân số mới bằng phân số đã cho.

* So sánh các phân số

Để so sánh phân số, các em cần lưu ý:

1. So sánh các phân số có cùng mẫu số

• Phân số nào có tử số nhỏ hơn thì phân số đó sẽ nhỏ hơn.

• Phân số nào có tử số lớn hơn thì phân số đó sẽ lớn hơn.

• Nếu hai phân số có tử số bằng nhau thì hai phân số đó sẽ bằng nhau.

2. So sánh các phân số có cùng tử số

• Phân số nào có mẫu số nhỏ hơn thì phân số đó sẽ lớn hơn.

• Phân số nào có mẫu số lớn hơn thì phân số đó nhỏ sẽ hơn.

• Nếu hai phân số có mẫu số bằng nhau thì hai phân số đó sẽ bằng nhau.

3. So sánh các phân số khác mẫu số

Để so sánh hai phân số khác mẫu số thì cần phải quy đồng mẫu số hai phân số đó rồi so sánh các tử số của hai phân số mới.

* Các phép tính phân số

Cũng tương tự như các số tự nhiên, với phân số cũng sẽ có những phép tính cơ bản sau:

1. Phép cộng phân số

• Để cộng 2 phần số cùng mẫu, ta chỉ cần cộng tử với tử số và giữ nguyên mẫu số.

• Để cộng 2 phân số khác mẫu, ta quy đồng mẫu số của hai phân số rồi tiến hành cộng hai phân số mới với nhau.

2. Phép trừ phân số

• Để cộng 2 phần số cùng mẫu, ta chỉ cần trừ tử số phân số thứ nhất cho tử số của phân số thứ 2 và giữ nguyên mẫu số.

• Để trừ 2 phân số khác mẫu, ta quy đồng mẫu số của hai phân số rồi tiến hành trừ hai phân số mới với nhau.

3. Phép nhân phân số

Để nhân hai phân số, ta lấy tử số phân số thứ nhất nhân với tử số thứ hai và mẫu số phân số thứ nhất nhân với mẫu số phân số thứ hai.

4. Phép chia phân số

Để chia hai phân số, là lấy phân số thứ nhất nhân với nghịch đảo phân số thứ 2. Trong đó, nghịch đảo phân số chính là phân số đảo ngược tử thành mẫu và mẫu thành tử.

* Tìm phân số của một số

Để tìm phân số của một số, ta lấy số đó nhân với phân số đã cho.

Công thức: giá trị a/b của A = A × a/b

Ví dụ: Trong rổ có 12 quả cam. Hỏi 2/3 số cam trong rổ là bao nhiêu?

Giải

2/3 Số cam trong rổ là:

12 × 2/3 = 8 (quả)

Đáp số: 8 quả

* Tìm một số biết giá trị phân số của số đó

Để một số khi biết một giá trị phân số của số đó, ta lấy giá trị đó chia cho phân số.

Giá trị a/b của A = giá trị của phân số : a/b

Ví dụ: Cho 2/3 số cam trong rổ cam là 8 quả. Hỏi rổ cam đó có bao nhiêu quả?

Giải

Số cam trong rổ là:

8 : 2/3 = 12 (quả)

Đáp số: 12 quả

Ôn tập tìm hai số khi biết tổng hoặc hiệu và tỉ của hai số đó

Một trong những chủ đề mà các em sẽ học trong chương trình toán lớp 4 khá quan trọng, chính là việc giải bài tập tìm 2 số khi biết tổng hoặc hiệu và tỉ số của chúng. Để chinh phục được dạng bài tập này, các em cần ghi nhớ các quy tắc sau:

* Tổng và hiệu

• Số bé = (Tổng – Hiệu) : 2

• Số lớn = (Tổng + Hiệu) : 2

Ví dụ: Tìm hai số biết tổng của hai số đó là 90. Hiệu của hai số là 34.

Cách giải:

Số bé là: (90 – 34) : 2 = 28

Số lớn là: (90 + 34) : 2 = 62

Vậy số bé là 28 và số lớn là 62.

* Tổng và tỉ

Các bước giải bài toán khi biết tổng và tỉ số:

• Bước 1: Ta phải xác định tổng và tỉ số đã cho rồi biểu diễn chúng trên sơ đồ đoạn thẳng, tóm tắt bài toán.

• Bước 2: Dựa vào sơ đồ đoạn thẳng để tiến hành tìm tổng số bằng nhau.

• Bước 3: Tìm giá trị phần cần tìm trong bài toán

• Bước 4: Tìm số lớn (hoặc số bé)

• Bước 5: Tìm số bé (hoặc số lớn), trình bày lời giải và ghi đáp số

Ví dụ: Tìm hai số biết tổng của hai số đó là 84. Tỉ số của hai số đó là 2/5.

Hướng dẫn giải:

Ta có sơ đồ như sau:

Tổng số phần bằng nhau là: 2 + 5 = 7 (phần)

Giá trị của một phần là: 84 : 7 = 12

Số bé là: 12 x 2 = 24

Số lớn là: 12 x 5 = 60

Vậy số bé là 24 và số lớn là 60.

* Hiệu và tỉ

Các bước giải bài toán khi biết hiệu và tỉ số:

• Bước 1: Xác định giá trị hiệu và tỉ số của bài toán, rồi biểu diễn chúng trên sơ đồ đoạn thẳng và tóm tắt bài toán.

• Bước 2: Dựa vào sơ đồ đoạn thẳng để tìm hiệu số phần bằng nhau

• Bước 3: Tìm giá trị một phần trong bài toán

• Bước 4: Tìm số lớn (hoặc số bé)

• Bước 5: Tìm số bé (hoặc số lớn), trình bày lời giải và ghi đáp số

Ví dụ: Tìm hai số bé hiệu của hai số đó là 56. Tỉ số của hai số đó là ⅗. 

Hướng dẫn giải:

Ta có sơ đồ đoạn thẳng như sau:

Hiệu số phần bằng nhau là: 5 – 3 = 2 (phần)

Giá trị của một phần là: 56 : 2 = 28

Số bé là: 28 x 3 = 84

Số lớn là: 28 x 5 = 140

Vậy số bé là 84 và số lớn là 140.

Bí quyết học các quy tắc toán học lớp 4 hiệu quả

Các quy tắc, công thức toán học lớp 4 cơ bản khá nhiều. Nên để giúp bé học tốt những kiến thức này, dưới đây là một số bí quyết mà phụ huynh có thể tham khảo thêm để hỗ trợ trẻ:

• Học tới đâu chắc đến đó: Thay vì cho bé học quá nhiều, bố mẹ nên đảm bảo con học phần kiến thức nào phải chắc chắn phần đó. Nếu bé quên hay gặp khó khăn phần nào thì phụ huynh cần hướng dẫn, củng cố lại kịp thời.

• Học toán lớp 4 theo sơ đồ tư duy: Đây là phương pháp được nhiều giáo viên khuyến khích học sinh áp dụng. Để giúp bé dễ dàng tiếp thu, ghi nhớ và tư duy tốt hơn khi học toán thì phụ huynh có thể hướng dẫn bé vẽ sơ đồ tư duy từng phần kiến thức và ôn luyện theo từng nhánh sơ đồ riêng sẽ hiệu quả hơn.

• Tích cực luyện tập, thực hành thường xuyên: Bên cạnh việc nắm chắc lý thuyết, phụ huynh nên khuyến khích, yêu cầu bé thực hành nhiều hơn từ làm bài tập trong SGK, sách bài tập, tìm hiểu thêm nhiều kiến thức trên internet, luyện đề thi, ứng dụng trong thực tiễn, chơi trò chơi… Qua đó sẽ giúp nâng cao hiệu quả tiếp thu, ghi nhớ và tư duy học toán tốt hơn.

• Xây dựng nền tảng toán học vững chắc cùng Monkey Math: Đây là ứng dụng dạy toán song ngữ dành cho trẻ mầm non và tiểu học, với hơn 400 bài giảng bám sát chương trình GDPT mới nhất của Bộ đưa ra, cùng với hơn 60 chủ đề toán, 4 cấp độ từ dễ đến khó sẽ giúp bé dễ dàng tiếp thu được với những kiến thức theo phương pháp hiện đại hơn. Đồng thời, tất cả bài giảng đều biên soạn dưới dạng video, hình ảnh hoạt hoạ ngộ nghĩnh, kết hợp cùng với đa dạng trò chơi tương tác giúp bé vừa chơi, vừa học hiệu quả hơn. Chưa kể, Monkey Math còn xây dựng nhiều tính năng hỗ trợ bé học toán một cách bài bản hơn, bố mẹ dễ dàng theo dõi và quản lý năng lực học tập của bé hiệu quả thông qua app.

Để hiểu rõ hơn về Monkey Math, quý phụ huynh có thể đăng ký để nhận được tư vấn miễn phí hoặc theo dõi video sau:

 

Kết luận

Trên đây là tổng hợp các quy tắc toán học lớp 4 để phụ huynh và các bé tham khảo. Đây đều là những quy tắc cơ bản nhưng quan trọng, không chỉ học ở lớp 4 mà các lớp cao hơn hay thực tế vẫn sử dụng đến. Vậy nên, phụ huynh hãy cùng con em mình cùng nhau học tập, ôn luyện để chinh phục môn toán một cách hiệu quả nhất nhé.